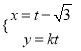题目内容
【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,
, ![]() 轴被曲线
轴被曲线![]() 截得的线段长等于
截得的线段长等于![]() 的长半轴长。
的长半轴长。
(1)求![]() ,
, ![]() 的方程;
的方程;
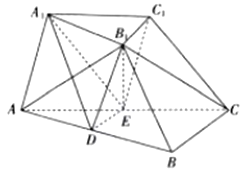
(2)设![]() 与
与![]() 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线![]() 与
与![]() 相交于点A,B,直线MA,MB分别与
相交于点A,B,直线MA,MB分别与![]() 相交与D,E.
相交与D,E.
①证明: ![]() ;
;
②记△MAB,△MDE的面积分别是![]() .问:是否存在直线
.问:是否存在直线![]() ,使得
,使得![]() =
=![]() ?请说明理由。
?请说明理由。
【答案】(1)![]()
(2)①见解析 ②满足条件的直线![]() 存在,且有两条,其方程分别为
存在,且有两条,其方程分别为![]() 和
和![]()
【解析】(1)由题意知![]() ,从而
,从而![]() ,又
,又![]() ,解得
,解得![]() 。
。
故![]() ,
, ![]() 的方程分别为
的方程分别为![]() 。
。
(2)①由题意知,直线![]() 的斜率存在,设为
的斜率存在,设为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .
.
由![]() 得
得![]() ,
,
设![]() ,则
,则![]() 是上述方程的两个实根,于是
是上述方程的两个实根,于是![]() 。
。
又点![]() 的坐标为
的坐标为![]() ,所以
,所以
![]()
故![]() ,即
,即![]() 。
。
②设直线的斜率为![]() ,则直线的方程为
,则直线的方程为![]() ,由
,由![]() 解得
解得![]() 或
或![]() ,则点的坐标为
,则点的坐标为![]()
又直线![]() 的斜率为
的斜率为![]() ,同理可得点B的坐标为
,同理可得点B的坐标为 .
.
于是
由![]() 得
得![]() ,
,
解得![]() 或
或 ,则点
,则点![]() 的坐标为
的坐标为 ;
;
又直线的斜率为![]() ,同理可得点
,同理可得点![]() 的坐标
的坐标
于是
因此
由题意知,  解得
解得![]() 或
或![]() 。
。
又由点![]() 的坐标可知,
的坐标可知, 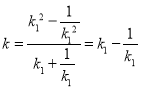 ,所以
,所以![]()
故满足条件的直线![]() 存在,且有两条,其方程分别为
存在,且有两条,其方程分别为![]() 和
和![]() 。
。

【题目】2017年是某市大力推进居民生活垃圾分类的关键一年,有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识”的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图所示:
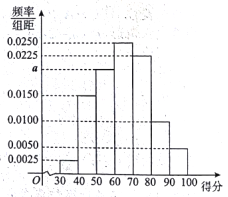
(Ⅰ)估计该组数据的中位数、众数;
(Ⅱ)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布N(μ,210),μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(50.5<Z<94);
(Ⅲ)在(Ⅱ)的条件下,有关部门为此次参加问卷调査的市民制定如下奖励方案:
(i)得分不低于μ可获赠2次随机话费,得分低于μ则只有1次;
(ii)每次赠送的随机话费和对应概率如下:
赠送话费(单元:元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加.问卷调查获赠的话费,求X的分布列和数学期望.
附: ![]() ,
,
若ZN(μ,σ2),则P(μ-σ<Z<μ+σ)= 0.6826,P(μ-2σ<Z<μ+2σ)=0.9544.