题目内容
【题目】如图, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 是等边三角形,
是等边三角形, ![]() ,
,
![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:⑴证明![]() ,
, ![]() ,推出
,推出![]() 平面
平面![]() ,然后证明
,然后证明
![]() ;
;
⑵以点![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 且与直线
且与直线![]() 平行的直线为
平行的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,说明
,说明![]() 为直线
为直线![]() 与平面
与平面![]() 所成角,设
所成角,设![]() ,求出相关点的坐标,求出平面
,求出相关点的坐标,求出平面![]() 与平面
与平面![]() 的法向量,利用空间向量的数量积求解即可;
的法向量,利用空间向量的数量积求解即可;
解析:(1)因为![]() 是等边三角形,
是等边三角形, ![]() 是
是![]() 的中点,所
的中点,所![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)法1:以点![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 且与直线
且与直线![]() 平行的直线为
平行的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成角.
所成角.
得![]() ,即
,即![]() ,从而
,从而![]() .
.
不妨设![]() ,又
,又![]() ,则
,则![]() ,
, ![]() .故
.故![]() ,
, ![]() ,
,
![]() ,
, ![]() .于是
.于是![]() ,
,
![]() ,
, ![]() ,
, ![]() ,设平面
,设平面![]() 与平面
与平面![]() 的法向量分别为
的法向量分别为
![]() ,
, ![]() ,由
,由![]() 得
得 令
令![]() ,得
,得![]() ,
,
所以![]() .由
.由![]() 得
得 令
令![]() 得
得
![]() ,
, ![]() .所以
.所以 .
.
所以![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
法2:因为![]() 平面
平面![]() ,所以
,所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成角.
所成角.
由题意得![]() ,即
,即![]() ,从而
,从而![]() .
.
不妨设![]() ,又
,又![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
由于![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,则
,则![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() .
.
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() . 所以
. 所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,在
,在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,因为
,因为![]() ,
,
所以![]() .所以二面角
.所以二面角![]() 的余弦值
的余弦值![]()


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案【题目】某动漫影视制作公司长期坚持文化自信,不断挖掘中华优秀传统文化中的动漫题材,创作出一批又一批的优秀动漫影视作品,获得市场和广大观众的一致好评.同时也为公司赢得丰厚的利润,该公司2013年至2019年的年利润![]() 关于年份代号
关于年份代号![]() 的统计数据如下表(已知该公司的年利润与年份代号线性相关)
的统计数据如下表(已知该公司的年利润与年份代号线性相关)
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
年利润 | 29 | 33 | 36 | 44 | 48 | 52 | 59 |
(1)求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年的年利润;
的线性回归方程,并预测该公司2020年的年利润;
(2)当统计表中某年年利润的实际值大于由(1)中线性回归方程计算出该年利润的估计值时,称该年为A级利润年,否则称为B级利润年.现从2015年至2019年这5年中随机抽取2年,求恰有1年为A级利润年的概率.
参考公式: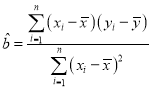 ,
,![]()
【题目】2017年是某市大力推进居民生活垃圾分类的关键一年,有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识”的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图所示:
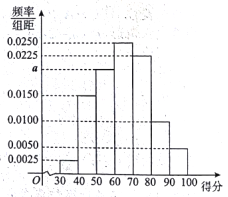
(Ⅰ)估计该组数据的中位数、众数;
(Ⅱ)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布N(μ,210),μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(50.5<Z<94);
(Ⅲ)在(Ⅱ)的条件下,有关部门为此次参加问卷调査的市民制定如下奖励方案:
(i)得分不低于μ可获赠2次随机话费,得分低于μ则只有1次;
(ii)每次赠送的随机话费和对应概率如下:
赠送话费(单元:元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加.问卷调查获赠的话费,求X的分布列和数学期望.
附: ![]() ,
,
若ZN(μ,σ2),则P(μ-σ<Z<μ+σ)= 0.6826,P(μ-2σ<Z<μ+2σ)=0.9544.

