题目内容
已知圆O的方程为x2+y2=3,且P(x,y)是圆O上任意一点,则
的取值范围______.
| x+y-5 |
| x-2 |
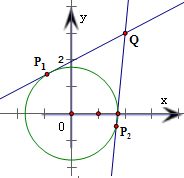
∵圆O的方程为x2+y2=3,∴圆心为O(0,0),半径r=
.
设z=
=1+
,设Q(2,3),
∵P(x,y)是圆O:x2+y2=3上任意一点,
∴k=
,表示P、Q两点连线的斜率.
设PQ的方程为y-3=k(x-2),即kx-y-2k+3=0.
由点O到直线PQ的距离小于或等于半径,
得
≤
,解之得6-
≤k≤6+
,
因此,可得z=
=1+k∈[7-
,7+
].
故答案为:[7-
,7+
]
| 3 |

设z=
| x+y-5 |
| x-2 |
| y-3 |
| x-2 |
∵P(x,y)是圆O:x2+y2=3上任意一点,
∴k=
| y-3 |
| x-2 |
设PQ的方程为y-3=k(x-2),即kx-y-2k+3=0.
由点O到直线PQ的距离小于或等于半径,
得
| |-2k+3| | ||
|
| 3 |
| 30 |
| 30 |
因此,可得z=
| x+y-5 |
| x-2 |
| 30 |
| 30 |
故答案为:[7-
| 30 |
| 30 |

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
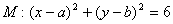 与圆
与圆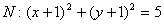 的两个交点始终为圆
的两个交点始终为圆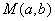 的轨迹方程为 .
的轨迹方程为 .