题目内容
【题目】如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( ) 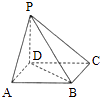
A.30°
B.45°
C.60°
D.90°
【答案】C
【解析】解:如图,以D为坐标原点,DA所在直线为x轴,DC所在线为y轴,DP所在线为z轴,建立空间坐标系, ∵点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,令PD=AD=1
∴A(1,0,0),P(0,0,1),B(1,1,0),D(0,0,0)
∴ ![]() =(1,0,﹣1),
=(1,0,﹣1), ![]() =(﹣1,﹣1,0)
=(﹣1,﹣1,0)
∴cosθ= 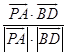 =
= ![]()
故两向量夹角的余弦值为 ![]() ,即两直线PA与BD所成角的度数为60°.
,即两直线PA与BD所成角的度数为60°.
故选C
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
【题目】为了促进学生的全面发展,郑州市某中学重视学生社团文化建设,现用分层抽样的方法从“话剧社”,“创客社”,“演讲社”三个金牌社团中抽取6人组成社团管理小组,有关数据见表(单位:人):
社团名称 | 成员人数 | 抽取人数 |
话剧社 | 50 | a |
创客社 | 150 | b |
演讲社 | 100 | c |
(1)求a,b,c的值;
(2)若从“话剧社”,“创客社”,“演讲社”已抽取的6人中任意抽取2人担任管理小组组长,求这2人来自不同社团的概率.
