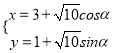题目内容
【题目】在如图所示的几何体中,四边形ABCD为正方形, ![]() 为直角三角形,
为直角三角形, ![]() ,且
,且![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求异面直线BE与AC所成角的余弦值.
【答案】(1)详见解析;(2)![]() .
.
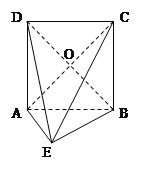
【解析】试题分析:(1)由已知可知AE⊥AB,又AE⊥AD,所以AE⊥平面ABCD,所以AE⊥DB,又ABCD为正方形,所以DB⊥AC,所以DB⊥平面AEC,而BD![]() 平面BED,故有平面AEC⊥平面BED.
平面BED,故有平面AEC⊥平面BED.
(2)作DE的中点F,连接OF,AF,由于O是DB的中点,且OF∥BE,可知∠FOA或其补角是异面直线BE与AC所成的角;设正方形ABCD的边长为2![]() ,则
,则![]() ,由于
,由于![]() ,AB=2AE,
,AB=2AE,
可知![]() ,
, ![]() ,则
,则![]() ,又
,又![]() ,∴
,∴![]() =
= ![]() ,由余弦定理的推理∴
,由余弦定理的推理∴![]() ∠FOA=
∠FOA=![]() =
=![]() ,故异面直线BE与AC所成的角的余弦值为
,故异面直线BE与AC所成的角的余弦值为![]() .
.
试题解析:(1)由已知有AE⊥AB,又AE⊥AD,
所以AE⊥平面ABCD,所以AE⊥DB, 3分
又ABCD为正方形,所以DB⊥AC, 4分
所以DB⊥平面AEC,BD![]() 面BED
面BED
故有平面AEC⊥平面BED. 6分
(2)作DE的中点F,连接OF,AF,
∵O是DB的中点,
∴OF∥BE,∴∠FOA或其补角是异面直线BE与AC所成的角。 8分
设正方形ABCD的边长为2![]() ,
,
则![]()
∵![]() ,AB=2AE,
,AB=2AE,
∴![]() ,
, ![]() ,∴
,∴![]() 10分
10分
又![]() ,∴
,∴![]() =
= ![]() ,∴
,∴![]() ∠FOA=
∠FOA=![]() =
=![]()
∴异面直线BE与AC所成的角的余弦值为![]() 12分.
12分.

【题目】某校90名专职教师的年龄状况如下表:
年龄 | 35岁以下 | 35~50岁 | 50岁以上 |
人数 | 45 | 30 | 15 |
现拟采用分层抽样的方法从这90名专职教师中抽取6名老、中、青教师下乡支教一年.
(Ⅰ)求从表中三个年龄段中分别抽取的人数;
(Ⅱ)若从抽取的6个教师中再随机抽取2名到相对更加边远的乡村支教,计算这两名教师至少有一个年龄是35~50岁教师的概率。
【题目】某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
频率 | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为![]() ,等级系数为5的2件日用品记为
,等级系数为5的2件日用品记为![]() ,现从
,现从![]() ,
, ![]() 这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.
这5件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.