题目内容

3．如果椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1上一点P到它的左焦点的距离是2，那么点P到右焦点的距离为（　　）
A．2B．4C．6D．10

分析 根据椭圆的定义，|PF1|+|PF2|=2a，求出结果即可

解答 解：∵椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1，
∴当椭圆上的点P到它的左焦点的距离是2时，
点P到它的右焦点的距离是2a-2=2×4-2=6．
故选：C．

点评 本题考查了椭圆的定义与标准方程的应用问题，是基础题目．

练习册系列答案
相关题目
15．若数列{an}满足a1=1，an+$\frac{1}{{a}_{n}}$=2，求Sn．
14．已知函数f（x）=x-alnx，g（x）=-$\frac{1}{x}$，a∈R；
（1）设h（x）=f（x）+g（x），若h（x）在定义域内存在极值，求a的取值范围；
（2）设f′（x）是f（x）的导函数，若0＜x1＜x2，a≠0，f′（t）=$\frac{{f（{x_2}）-f（{x_1}）}}{{{x_2}-{x_1}}}$（x1＜t＜x2），求证：t＜$\frac{{{x_1}+{x_2}}}{2}$．
11．已知椭圆的离心率为$\frac{\sqrt{3}}{2}$，且过点（2，0），则椭圆的标准方程$\frac{{x}^{2}}{4}+{y}^{2}=1$或$\frac{{y}^{2}}{16}+\frac{{x}^{2}}{4}=1$．
18．已知点P在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，F1F2分别是其左、右焦点，若|PF1|=2|PF2|，则该椭圆的离心率的取值范围是（　　）
A．（0，$\frac{1}{3}$]B．（$\frac{1}{3}$，1）C．（0，$\frac{1}{3}$）D．[$\frac{1}{3}$，1）
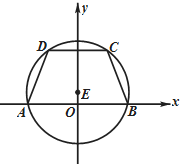8．如图所示，等腰梯形ABCD的底边AB在x轴上，顶点A与顶点B关于原点O对称，且底边AB和CD的长分别为6和2$\sqrt{6}$，高为3．
（Ⅰ）求等腰梯形ABCD的外接圆E的方程；
（Ⅱ）若点N的坐标为（5，2），点M在圆E上运动，
求线段MN的中点P的轨迹方程．
15．已知△ABC三个顶点分别为A（1，0），B（1，4），C（3，2），直线l经过点（0，4）．
（1）求证：△ABC是等腰直角三角形；
（2）求△ABC外接圆⊙M的方程；
（3）若直线l与⊙M相交于P，Q两点，且PQ=2$\sqrt{3}$，求直线l的方程．
12．已知点N（4，0），点M（x0，y0）在圆x2+y2=4上运动，点P（x，y）为线段MN的中点．
（Ⅰ）求点P（x，y）的轨迹方程；
（Ⅱ）求点P到直线3x+4y-56=0的距离的最大值和最小值．
13．已知F1、F2是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的两焦点，过点F1的直线交椭圆于A、B两点，在△AF1B中，若有两边之和是10，则第三边的长度为（　　）
A．3B．4C．5D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网