题目内容

16．设M（x0，y0）为抛物线C：y2=8x上一点，F为C的焦点，若以F为圆心，|FM|为半径的圆和C的准线相交，则x0的取值范围是（2，+∞）．

分析 由条件|FM|＞4，由抛物线的定义|FM|可由x0表达，由此可求x0的取值范围．

解答 解：由条件以F为圆心，|FM|为半径的圆和抛物线C的准线相交，可得|FM|＞4，
由抛物线的定义|FM|=x0+2＞4，所以x0＞2
故答案为：（2，+∞）．

点评 本题考查直线和圆的位置关系、抛物线的定义的运用，考查学生分析解决问题的能力，属于基础题．

练习册系列答案
相关题目
19．设复数z的虚部记作lm（z），已知i为虚数单位，则lmz=lm（$\frac{13}{2i+3}$）=（　　）
A．-3B．3C．-2D．2
20．函数f（x）=log（3-x）（x-1）的定义域用区间表示为x∈（1，2）∪（2，3）．
4．已知正三棱锥P-ABC的侧棱与底面所成的角为45°，求相邻两侧面所成角的余弦值．
11．在复平面内，复数z与$\frac{2}{1-i}$的对应点关于虚轴对称，则z=-1+i．
1．双曲线$\frac{x^2}{13}-\frac{y^2}{3}=1$的渐近线与圆（x-4）2+y2=r2（r＞0）相切，则r=（　　）
A．4B．3C．2D．$\sqrt{3}$
8．已知点F（1，0），点P为平面上的动点，过点P作直线l：x=-1的垂线，垂足为H，且$\overrightarrow{HP}$•$\overrightarrow{HF}$=$\overrightarrow{FP}$•$\overrightarrow{FH}$．
（1）求动点P的轨迹C的方程；
（2）过点F的直线与轨迹C交于点A，B两点，在A，B处分别作轨迹C的切线交于点N，求证：kNF•kAB为定值．
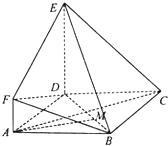5．如图，四边形ABCD是菱形，DE⊥DC，平面DEC⊥平面ABCD．
（Ⅰ）求证：AC⊥平面BDE；
（Ⅱ）若AF∥DE，AF=$\frac{1}{3}$DE，点M在线段BD上，且DM=$\frac{2}{3}$BD，求证：AM∥平面BEF．
6．某抛物线的通径与圆x2+y2-4x+2y-11=0的半径相等，则该抛物线的焦点到其准线的距离为（　　）
A．2B．4C．6D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网