题目内容
20.已知原命题:“若a+b≥2,则a,b 中至少有一个不小于1”,则原命题与其否命题的真假情况是( )| A. | 原命题为真,否命题为假 | B. | 原命题为假,否命题为真 | ||
| C. | 原命题与否命题均为真命题 | D. | 原命题与否命题均为假命题 |
分析 容易看出原命题为真,加以说明即可,写出其否命题,再判断真假即可,对于假命题的情况,举反例即可.
解答 解:原命题为真,∵若结论不成立,即a,b都小于1,这样便不满足a+b≥2;
它的否命题为:“若a+b<2,则a,b都小于1”,该命题为假,比如,a=2>1,b=-2,满足a+b<2.
故选A.
点评 考查原命题、否命题的概念,注意学会本题在说明原命题为真命题时用的方法:假设为假,说明假设不成立即可,以及用举反例的方法说明一个命题为假命题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
3.已知点A=(-1,1)、B=(1,2)、C=(-3,2),则向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | -$\frac{3\sqrt{5}}{5}$ | D. | $\frac{3}{5}$ |
15.从点P出发的三条射线PA,PB,PC两两成60°角,且分别与球O相切于A,B,C三点,若OP=$\sqrt{3}$,则球的体积为( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{8π}{3}$ |
12.某工厂从外地连续两次购得A,B两种原料,购买情况如右表:现计划租用甲,乙两种货车共8辆将两次购得的原料一次性运回工厂.
(1)A,B两种原料每吨的进价各是多少元?
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
| A(吨) | B(吨) | 费用(元) | |
| 第一次 | 12 | 8 | 33600 |
| 第二次 | 8 | 4 | 20800 |
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
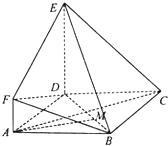 如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.
如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.