题目内容
15.设函数f(x)=(x+a)lnx,g(x)=.已知曲线y=f(x)在点(1,f(1))处的切线与直线2x-y=0平行.(Ⅰ)求a的值;
(Ⅱ)是否存在自然数k,使得方程f(x)=g(x)在(k,k+1)内存在唯一的根?如果存在,求出k;如果不存在,请说明理由;
(Ⅲ)设函数m(x)=min{f(x),g(x)}(min{p,q}表示p,q中的较小值),求m(x)的最大值.
分析 (Ⅰ)求出f(x)的导数,求得切线的斜率,由两直线平行的条件:斜率相等,解方程可得a=1;
(Ⅱ)求出f(x)、g(x)的导数和单调区间,最值,由零点存在定理,即可判断存在k=1;
(Ⅲ)由(Ⅱ)求得m(x)的解析式,通过g(x)的最大值,即可得到所求.
解答 解:(Ⅰ)函数f(x)=(x+a)lnx的导数为f′(x)=lnx+1+,
曲线y=f(x)在点(1,f(1))处的切线斜率为f′(1)=1+a,
由切线与直线2x-y=0平行,
则a+1=2,解得a=1;
(Ⅱ)由(Ⅰ)可得f(x)=(x+1)lnx,f′(x)=lnx+1+,
令h(x)=lnx+1+,h′(x)=-=,
当x∈(0,1),h′(x)<0,h(x)在(0,1)递减,
当x>1时,h′(x)>0,h(x)在(1,+∞)递增.
当x=1时,h(x)min=h(1)=2>0,即f′(x)>0,
f(x)在(0,+∞)递增,即有f(x)在(k,k+1)递增,
g(x)=的导数为g′(x)=,
当x∈(0,2),g′(x)>0,g(x)在(0,2)递增,
当x>2时,g′(x)<0,g(x)在(2,+∞)递减.
则x=2取得最大值,
令T(x)=f(x)-g(x)=(x+1)lnx-,
T(1)=-<0,T(2)=3ln2->0,
T(x)的导数为T′(x)=lnx+1+-,
由1<x<2,通过导数可得lnx>1-,即有lnx+1+>2;
ex>1+x,可得->,
可得lnx+1+->2+=>0,
即为T′(x)>0在(1,2)成立,
则T(x)在(1,2)递增,
由零点存在定理可得,存在自然数k=1,
使得方程f(x)=g(x)在(k,k+1)内存在唯一的根;
(Ⅲ)由(Ⅱ)知,m(x)=,其中x0∈(1,2),
且x=2时,g(x)取得最大值,且为g(2)=,
则有m(x)的最大值为m(2)=.
点评 本题考查导数的运用:求切线方程和单调区间、极值,同时考查零点存在定理和分段函数的最值,考查运算能力,属于中档题.

| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
| A. | -i | B. | -3i | C. | i | D. | 3i |
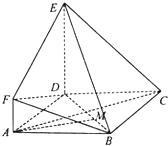 如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.
如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.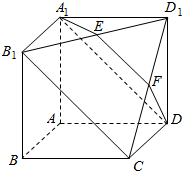 如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.
如图所示,在多面体A1B1D1DCBA中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.