题目内容
17.已知平面向量$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(4,m),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则向量$\overrightarrow{b}$在$\overrightarrow{a}$-$\overrightarrow{b}$方向上的投影为( )| A. | $\sqrt{5}$ | B. | -2$\sqrt{5}$ | C. | 4 | D. | -4 |
分析 首先利用向量垂直,得到数量积为0,求出m,然后表示出向量$\overrightarrow{b}$、$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,利用数量积公式解得.
解答 解:因为$\overrightarrow{a}$⊥$\overrightarrow{b}$,所以$\overrightarrow{a}$•$\overrightarrow{b}$=4-2m=0,解得m=2,则$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,-4),
则向量$\overrightarrow{b}$在$\overrightarrow{a}$-$\overrightarrow{b}$方向上的投影为|$\overrightarrow{b}$|cosθ=$\frac{(\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{a}-\overrightarrow{b}|}=\frac{-20}{5}$=-4;
故选D.
点评 本题考查了向量的垂直的性质以及一个向量在另一个向量上的投影;属于基础题.

练习册系列答案
相关题目
12.某工厂从外地连续两次购得A,B两种原料,购买情况如右表:现计划租用甲,乙两种货车共8辆将两次购得的原料一次性运回工厂.
(1)A,B两种原料每吨的进价各是多少元?
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
| A(吨) | B(吨) | 费用(元) | |
| 第一次 | 12 | 8 | 33600 |
| 第二次 | 8 | 4 | 20800 |
(2)已知一辆甲种货车可装4吨A种原料和1吨B种原料;一辆乙种货车可装A,B两种原料各2吨.如何安排甲,乙两种货车?写出所有可行方案.
(3)若甲种货车的运费是每辆400元,乙种货车的运费是每辆350元.设安排甲种货车x辆,总运费为W元,求W(元)与x(辆)之间的函数关系式;在(2)的前提下,x为何值时,总运费W最小,最小值是多少元?
2.如图所示程序框图,则满足|x|+|y|≤2的输出的有序实数对(x,y)的概率为( )


| A. | $\frac{1}{16}$ | B. | $\frac{3}{32}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
7.设i是虚数单位,则复数i3-$\frac{2}{i}$=( )
| A. | -i | B. | -3i | C. | i | D. | 3i |
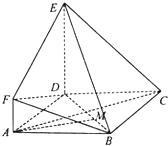 如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.
如图,四边形ABCD是菱形,DE⊥DC,平面DEC⊥平面ABCD.