题目内容
7.给出一个程序框图,则输出x的值是( )
| A. | 39 | B. | 41 | C. | 43 | D. | 45 |
分析 根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:S=5+7+…,当S≥480时,退出循环,输出x的值,由等差数列的求和公式及通项公式即可得解.
解答 解:根据流程图所示的顺序,
该程序的作用是累加并输出S=5+7+…的值,当S≥480时,退出循环,输出x的值.
设共有n个数相加,则由等差数列的求和公式可得:S=5n+$\frac{n(n-1)}{2}×2$≥480,解得:n≥20,
故由等差数列的通项公式可得最后一个x为:5+(20-1)×2=43.
即当x=43时,满足条件S≥480,退出循环,输出x的值为43.
故选:C.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.通过圆与球的类比,由“半径为R的圆的内接矩形中,以正方形的面积为最大,最大值为2R2”,猜想关于球的相应命题为( )
| A. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为2R3 | |
| B. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为3R3 | |
| C. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为$\frac{4\sqrt{3}}{9}$R3 | |
| D. | 半径为R的球的内接六面体中,以正方体的体积为最大,最大值为$\frac{8\sqrt{3}}{9}$R3 |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线均与圆C:x2+y2-6y+5=0相切,且双曲线的焦距为6,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
2. 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
12.执行如图所示的程序框图,则输出的S值为( )


| A. | 4 | B. | 6 | C. | 8 | D. | 16 |
19.按右图所示的程序框图运算,若输入 x=200,则输出 k 的值是( )
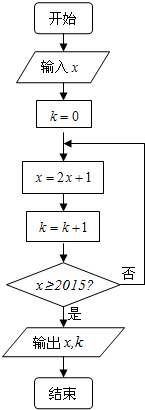

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.P是双曲线$\frac{x^2}{16}-\frac{y^2}{20}=1$上一点,F1,F2分别是双曲线左右焦点,若|PF1|=9,则|PF2|=( )
| A. | 1 | B. | 17 | C. | 1或17 | D. | 以上答案均不对 |