题目内容
10.双曲线C:x2-$\frac{{y}^{2}}{6}$=1的左焦点为F,双曲线与直线l:y=kx交于A、B两点,且∠AFB=$\frac{π}{3}$,则$\overrightarrow{FA}$•$\overrightarrow{FB}$=( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 求出双曲线的a,b,c,设双曲线的右焦点为F'.连AF',BF',可得四边形AFBF'为平行四边形,设AF=m,由双曲线的定义可得AF'=BF=m-2,运用余弦定理,可得m=4,再由向量的数量积的定义,计算即可得到所求.
解答 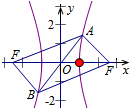 解:x2-$\frac{{y}^{2}}{6}$=1的a=1,b=$\sqrt{6}$,c=$\sqrt{7}$,
解:x2-$\frac{{y}^{2}}{6}$=1的a=1,b=$\sqrt{6}$,c=$\sqrt{7}$,
设双曲线的右焦点为F'.连AF',BF',
可得四边形AFBF'为平行四边形,
即有AF'=BF,∠FAF'=120°,
设AF=m,由双曲线的定义可得AF'=BF=m-2,
在△AFF'中,由余弦定理可得,
cos120°=$\frac{{m}^{2}+(m-2)^{2}-4×7}{2m(m-2)}$=-$\frac{1}{2}$,
解得m=4,
即AF=4,BF=2,
则$\overrightarrow{FA}$•$\overrightarrow{FB}$=|$\overrightarrow{FA}$|•|$\overrightarrow{FB}$|cos60°=4×2×$\frac{1}{2}$=4.
故选:B.
点评 本题考查双曲线的定义、方程和性质,考查余弦定理的运用,以及向量的数量积的定义,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.设F是双曲线$\frac{x^2}{4}$-$\frac{y^2}{12}$=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为( )
| A. | 5 | B. | 5+4$\sqrt{3}$ | C. | 7 | D. | 9 |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线均与圆C:x2+y2-6y+5=0相切,且双曲线的焦距为6,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
2.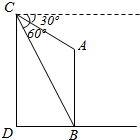 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
19.按右图所示的程序框图运算,若输入 x=200,则输出 k 的值是( )
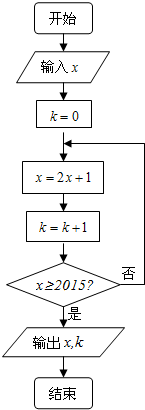

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.行如图所示的程序框图,若输入a=390,b=156,则输出a=( )
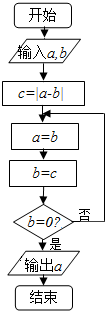

| A. | 26 | B. | 39 | C. | 78 | D. | 156 |