题目内容
13.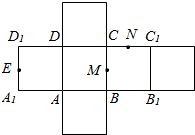 如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,
如图为正方体ABCD-A1B1C1D1的平面展开图,其中E、M、N分别为A1D1、BC、CC1的中点,(Ⅰ) 作出该正方体的水平放置直观图;
(Ⅱ) 求证:平面BEC1∥平面D1MN.
分析 (Ⅰ)根据该正方体的平面展开图及斜二测画法即可作出该正方体的水平放置的直观图;
(Ⅱ)根据中位线的性质便有MN∥BC1,从而得出MN∥平面BEC1,可以说明四边形BMD1E为平行四边形,从而得到MD1∥平面BEC1,从而由面面平行的判定定理即可得出平面BEC1∥平面D1MN.
解答 解:(Ⅰ)该正方体的水平放置直观图如下图所示: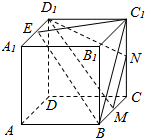
(Ⅱ)证明:M,N分别为BC,CC1的中点;
∴MN∥BC1,BC1?平面BEC1,MN?平面BEC1;
∴MN∥平面BEC1;
又E为A1D1中点;
∴ED1∥BM,且ED1=BM;
∴四边形BMD1E为平行四边形;
∴MD1∥BE;
∴MD1∥平面BEC1,MN∩MD1=M;
∴平面BEC1∥平面D1MN.
点评 考查正方体的水平放置的直观图的画法,由立体图形的平面展开图,可以画出其水平放置的直观图,以及中位线的性质,线面平行的判定定理,平行四边形的判定,面面平行的判定定理.

练习册系列答案
相关题目
4.身穿红、黄两种颜色衣服的各有两人,身穿蓝颜色衣服的有一人,现将这五人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
| A. | 24种 | B. | 48种 | C. | 36种 | D. | 28种 |
1.设F是双曲线$\frac{x^2}{4}$-$\frac{y^2}{12}$=1的左焦点,A(1,4),P是双曲线右支上的动点,则|PF|+|PA|的最小值为( )
| A. | 5 | B. | 5+4$\sqrt{3}$ | C. | 7 | D. | 9 |
8.程序框图中表示计算、赋值功能的是( )
| A. |  | B. |  | C. |  | D. |  |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的两条渐近线均与圆C:x2+y2-6y+5=0相切,且双曲线的焦距为6,则该双曲线的方程为( )
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{3}$=1 |
2.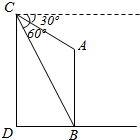 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
 如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )
如图,在山顶C测得山下塔顶A和塔底B的俯角分别为30°和60°,已知塔高AB为20m,则山高CD为( )| A. | 30m | B. | 20$\sqrt{3}$m | C. | $\frac{40\sqrt{3}}{3}$m | D. | 40m |
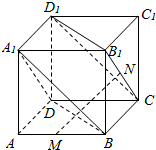 如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.
如图,正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点.