题目内容
三棱锥S—ABC的三条侧棱两两互相垂直,且SA=1,BS= ,SC=
,SC= ,则底面内的角∠ABC等于( )
,则底面内的角∠ABC等于( )
 ,SC=
,SC= ,则底面内的角∠ABC等于( )
,则底面内的角∠ABC等于( ) | A.30° | B.45° | C.60° | D.120° |
C
解:首先在侧面内求解底面的三边长,利用勾股定理可得分别为AB=2,BC=3,AC=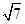 然后利用余弦定理可以求解∠ABC等于60°
然后利用余弦定理可以求解∠ABC等于60°
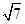 然后利用余弦定理可以求解∠ABC等于60°
然后利用余弦定理可以求解∠ABC等于60°
练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目

 (B)
(B) (C)
(C) (D)
(D)
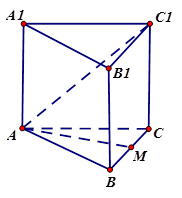
 中,
中, 是正方形ABCD的中心,
是正方形ABCD的中心, 、
、 分别是
分别是 、
、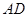 的中点, 异面直线
的中点, 异面直线 与
与 所成的角的余弦值是( )
所成的角的余弦值是( )






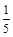
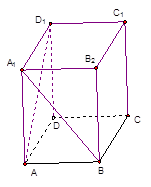
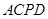 中,
中,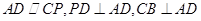 ,
,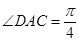 ,
,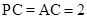 ,如图①;现将其沿
,如图①;现将其沿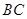 折成如图②的几何体,使得
折成如图②的几何体,使得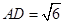 .
. 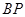 与平面
与平面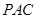 所成角的大小;(Ⅱ)求二面角
所成角的大小;(Ⅱ)求二面角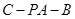 的余弦值.
的余弦值.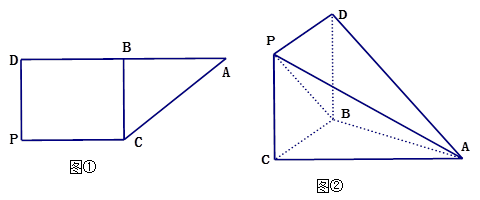
 为
为 ,直线
,直线 ,直线
,直线 ,则直线
,则直线 所成角的取值范围是 ( )
所成角的取值范围是 ( )



 的正方体
的正方体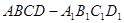 ,点
,点 、
、 分别是
分别是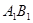 和
和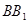 的中点,建立如图所示的空间直角坐标系.
的中点,建立如图所示的空间直角坐标系. 与
与 所成角的余弦值.
所成角的余弦值. 
 ,面SCD与面SAB所成二面角的正切值为
,面SCD与面SAB所成二面角的正切值为  。
。