题目内容
如图,正三棱柱ABC—A1B1C1的底面边长为a,点M在边 BC上,△AMC1是以点M为直角顶点的等腰直角三角形。
(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面AMC1的距离;
(Ⅲ)求二面角M—AC1—C的大小。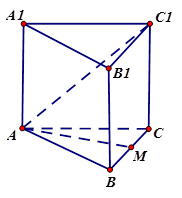
(Ⅰ)求证点M为边BC的中点;
(Ⅱ)求点C到平面AMC1的距离;
(Ⅲ)求二面角M—AC1—C的大小。

(Ⅰ)点M为BC边的中点
(Ⅱ)∴点C到平面AMC1的距离为底面边长为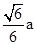
(Ⅲ)二面角M—AC1—C的大小为45°
(Ⅱ)∴点C到平面AMC1的距离为底面边长为
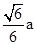
(Ⅲ)二面角M—AC1—C的大小为45°
本试题主要考查了立体几何中,空间点线面的位置关系的运用。第一问中,利用△AMC1为以点M为直角顶点的等腰直角三角形,∴AM⊥C1M且AM=C1M
又因为CC1⊥底面ABC∴C1M在底面内射影为CM,AM⊥CM。所以点M为BC边的中点
二问中,利用作辅助线,表示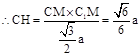 ,即为所求
,即为所求
三问中,过点C作CI⊥AC1于I,连HI,∵CH⊥平面C1AM,作出二面角的大小,然后借助于定义法得到结论。
(Ⅰ)∵△AMC1为以点M为直角顶点的等腰直角三角形,∴AM⊥C1M且AM=C1M
∵三棱柱ABC—A1B1C1,∴CC1⊥底面ABC∴C1M在底面内射影为CM,AM⊥CM。
∵底面ABC为边长为a的正三角形,∴点M为BC边的中点 --------------------4分
(Ⅱ)过点C作CH⊥MC1,由(Ⅰ)知AM⊥C1M且AM⊥CM,
∴AM⊥平面C1CM ∵CH在平面C1CM内,∴CH⊥AM,
∴CH⊥平面C1AM
由(Ⅰ)知,AM=CM= ,CM=
,CM=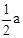
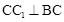
∴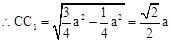 ∴
∴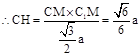
∴点C到平面AMC1的距离为底面边长为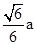 -------------------8分
-------------------8分
(Ⅲ)过点C作CI⊥AC1于I,连HI,∵CH⊥平面C1AM,
HI⊥AC1,∠CIH是二面角M—AC1—C的平面角
∴HI为CI在平面C1AM内的射影,
∴HI⊥AC1,∠CIH是二面角M—AC1—C的平面角,在直角三角形ACC1中 ,
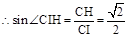 ∴∠CIH=45°, ∴二面角M—AC1—C的大小为45°
∴∠CIH=45°, ∴二面角M—AC1—C的大小为45°
又因为CC1⊥底面ABC∴C1M在底面内射影为CM,AM⊥CM。所以点M为BC边的中点
二问中,利用作辅助线,表示
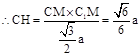 ,即为所求
,即为所求三问中,过点C作CI⊥AC1于I,连HI,∵CH⊥平面C1AM,作出二面角的大小,然后借助于定义法得到结论。
(Ⅰ)∵△AMC1为以点M为直角顶点的等腰直角三角形,∴AM⊥C1M且AM=C1M
∵三棱柱ABC—A1B1C1,∴CC1⊥底面ABC∴C1M在底面内射影为CM,AM⊥CM。
∵底面ABC为边长为a的正三角形,∴点M为BC边的中点 --------------------4分
(Ⅱ)过点C作CH⊥MC1,由(Ⅰ)知AM⊥C1M且AM⊥CM,
∴AM⊥平面C1CM ∵CH在平面C1CM内,∴CH⊥AM,
∴CH⊥平面C1AM
由(Ⅰ)知,AM=CM=
 ,CM=
,CM=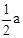
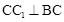
∴
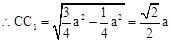 ∴
∴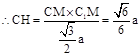
∴点C到平面AMC1的距离为底面边长为
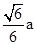 -------------------8分
-------------------8分(Ⅲ)过点C作CI⊥AC1于I,连HI,∵CH⊥平面C1AM,
HI⊥AC1,∠CIH是二面角M—AC1—C的平面角
∴HI为CI在平面C1AM内的射影,
∴HI⊥AC1,∠CIH是二面角M—AC1—C的平面角,在直角三角形ACC1中 ,
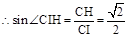 ∴∠CIH=45°, ∴二面角M—AC1—C的大小为45°
∴∠CIH=45°, ∴二面角M—AC1—C的大小为45°
练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目

 中,若
中,若 为直角,则有
为直角,则有 ;类比到三棱锥
;类比到三棱锥 中,若三个侧面
中,若三个侧面 两两垂直,且分别与底面所成的角为
两两垂直,且分别与底面所成的角为 ,则有
,则有 


 中,E是棱
中,E是棱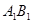 的中点,则异面直线
的中点,则异面直线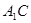 与AE所成角的余弦值是________.
与AE所成角的余弦值是________.
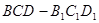 与四棱锥
与四棱锥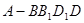 的组合体中,已知
的组合体中,已知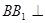 平面
平面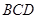 ,四边形
,四边形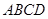 是平行四边形,
是平行四边形,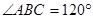 ,
,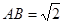 ,
,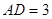 ,
,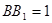 。
。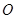 是线段
是线段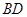 的中点,求证:
的中点,求证: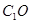 ∥平面
∥平面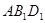 ;
;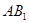 与平面
与平面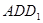 所成的角。
所成的角。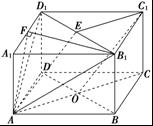
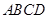 -
- 中,
中, 为
为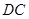 的中点,则
的中点,则 与
与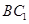 所在直线所成角的余弦值等于 ( ) ( )
所在直线所成角的余弦值等于 ( ) ( )




 ,SC=
,SC= ,则底面内的角∠ABC等于( )
,则底面内的角∠ABC等于( ) 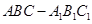 (三条侧棱和底面均垂直的三棱柱叫做直三棱柱)中,若
(三条侧棱和底面均垂直的三棱柱叫做直三棱柱)中,若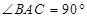 ,
,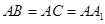 ,则异面直线
,则异面直线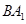 与
与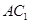 所成的角等于 ( )
所成的角等于 ( )