题目内容
如图(1),矩形ABCD中,M、N分别为边AD、BC的中点,E、F分别为边AB、CD上的定点且满足EB=FC,现沿虚线折叠使点B、C重合且与E、F共线,如图(2).若此时
二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )

(A) (B)
(B) (C)
(C) (D)
(D)
二面角A-MN-D的大小为60°,则折叠后EN与平面MNFD所成角的正弦值是( )

(A)
 (B)
(B) (C)
(C) (D)
(D)
D
过E作EQ//AM交MN于Q,连接FQ,则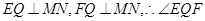
就是二面角A-MN-D所成角的平面角,所以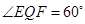 ,
,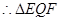 为等边三角形,
为等边三角形,
设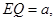 则
则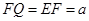 ,所以平面
,所以平面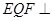 平面MNFD,取FQ的中点H,连接EH,HN,
平面MNFD,取FQ的中点H,连接EH,HN,
则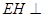 平面MNFD,所以
平面MNFD,所以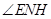 就是EN与平面MNFD所成角,因为
就是EN与平面MNFD所成角,因为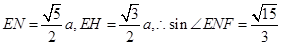 .
.
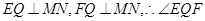
就是二面角A-MN-D所成角的平面角,所以
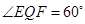 ,
,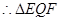 为等边三角形,
为等边三角形,设
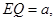 则
则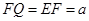 ,所以平面
,所以平面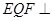 平面MNFD,取FQ的中点H,连接EH,HN,
平面MNFD,取FQ的中点H,连接EH,HN,则
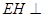 平面MNFD,所以
平面MNFD,所以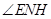 就是EN与平面MNFD所成角,因为
就是EN与平面MNFD所成角,因为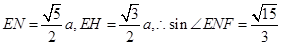 .
.
练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
 B
B 中,底面是菱形,
中,底面是菱形, BAD=60°,D B
BAD=60°,D B

 中,
中, ,E、F分别为
,E、F分别为 和AD的中点,则异面直线
和AD的中点,则异面直线 、EF所成的角为( )
、EF所成的角为( )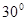



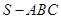 中,各个面都是边长为
中,各个面都是边长为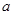 的正三角形,
的正三角形,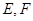 分别是
分别是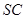 和
和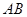 的中 点,则异面直线
的中 点,则异面直线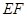 与
与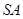 所成的角等于( )
所成的角等于( )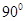 B
B 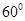 C
C 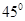 D
D 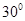
 中,若
中,若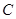 为直角,则有
为直角,则有 ;类比到三棱锥
;类比到三棱锥 中,若三个侧面
中,若三个侧面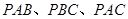 两两垂直,且分别与底面所成的角为
两两垂直,且分别与底面所成的角为 ,则有
,则有 
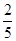


 ,SC=
,SC= ,则底面内的角∠ABC等于( )
,则底面内的角∠ABC等于( )