题目内容
(本题满分12分)已知,等差数列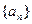 的首项
的首项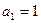 ,公差
,公差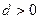 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列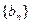 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列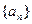
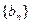 的通项公式;(2)设数列
的通项公式;(2)设数列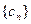 对任意正整数
对任意正整数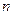 均有
均有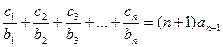 成立,求数列
成立,求数列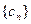 的前
的前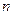 项的和
项的和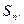
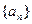 的首项
的首项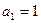 ,公差
,公差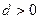 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列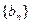 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列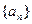
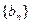 的通项公式;(2)设数列
的通项公式;(2)设数列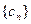 对任意正整数
对任意正整数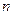 均有
均有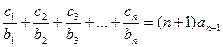 成立,求数列
成立,求数列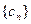 的前
的前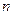 项的和
项的和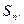
(Ⅰ)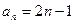
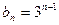 (Ⅱ)
(Ⅱ) 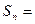
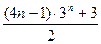
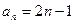
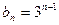 (Ⅱ)
(Ⅱ) 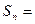
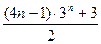
(1)由题意,得: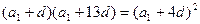 ,整理得:
,整理得: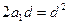
∵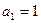 ,解得
,解得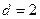 (∵
(∵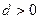 ,∴舍去
,∴舍去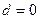 ).∴
).∴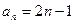 ,(
,(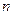 =1,2,…)
=1,2,…)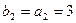 ,
,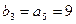 ,易求
,易求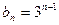 。(
。(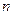 =1,2,3,…)(5′)
=1,2,3,…)(5′)
(2)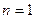 时,
时,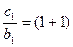 ·
·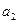 ,∴
,∴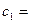 1
1 2
2 3=6.
3=6.
当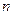 ≥2时,
≥2时,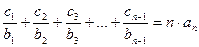 ,(8′)
,(8′)
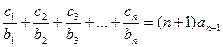 。
。
两式相减得: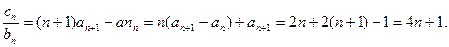
∴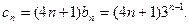 ∴
∴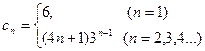 (10′)
(10′)
故当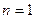 时,
时,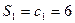 ,
,
当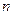 ≥2时,
≥2时,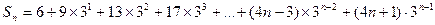
令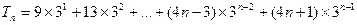 ,错位相消可得,
,错位相消可得,
∴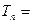
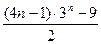 ∴
∴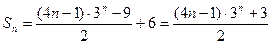
即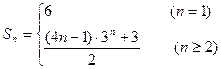 故
故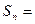
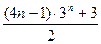 。(12′)
。(12′)
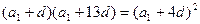 ,整理得:
,整理得: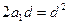
∵
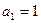 ,解得
,解得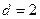 (∵
(∵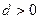 ,∴舍去
,∴舍去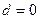 ).∴
).∴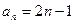 ,(
,(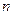 =1,2,…)
=1,2,…)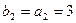 ,
,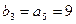 ,易求
,易求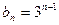 。(
。(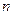 =1,2,3,…)(5′)
=1,2,3,…)(5′)(2)
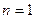 时,
时,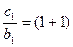 ·
·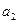 ,∴
,∴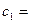 1
1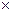 2
2 3=6.
3=6.当
 ≥2时,
≥2时,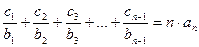 ,(8′)
,(8′)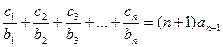 。
。两式相减得:
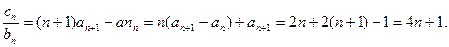
∴
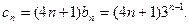 ∴
∴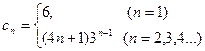 (10′)
(10′)故当
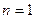 时,
时,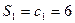 ,
,当
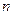 ≥2时,
≥2时,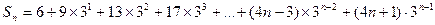
令
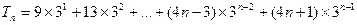 ,错位相消可得,
,错位相消可得,∴
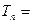
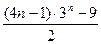 ∴
∴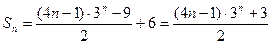
即
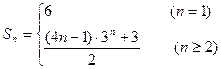 故
故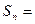
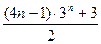 。(12′)
。(12′)
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
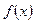 =
=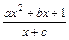 (a>0)为奇函数,且
(a>0)为奇函数,且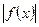 min=
min=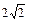 ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, 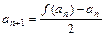 ,
,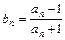 .
.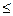
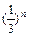 .
.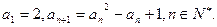
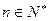 时,恒有
时,恒有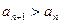 成立;
成立;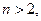 且
且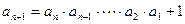 成立;
成立;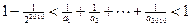 .
.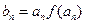 ,记数列
,记数列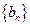 的前n项和为
的前n项和为 ,当
,当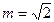 时,求
时,求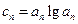 ,问是否存在实数
,问是否存在实数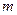 ,使得
,使得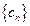 中每一项恒小于它后面的项?若存
中每一项恒小于它后面的项?若存

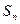

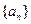 的公差
的公差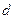 不为零,首项
不为零,首项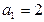 且前
且前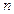 项和为
项和为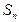 .
.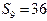 时,在数列
时,在数列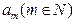 ,使得
,使得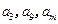 成为等比数列,求
成为等比数列,求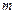 的值.
的值.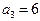 时,若自然数
时,若自然数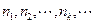 满足
满足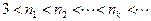 并且
并且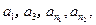
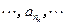 是等比数列,求
是等比数列,求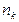 的值。
的值。