题目内容
【题目】已知椭圆C的中心在原点，离心率等于
，它的一个短轴端点恰好是抛物线
的焦点．
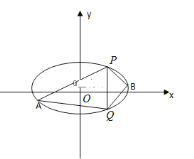
（1）求椭圆C的方程；
（2）已知P（2，3）、Q（2，﹣3）是椭圆上的两点，A，B是椭圆上位于直线PQ两侧的动点，若直线AB的斜率为，求四边形APBQ面积的最大值；
【答案】（1）
； （2）
.
【解析】
（1）根据椭圆离心率等于
，它的一个短轴端点恰好是抛物线
的焦点，结合性质
，列出关于
、
、
的方程组，求出 、，即可得结果；（2）设
，
的方程为
，联立方程得
，四边形
的面积
，从而可得结果.
（1）设C方程为
，
因为椭圆一个短轴端点恰好是抛物线的焦点。
所以
．由
，
，得a=4 ，
∴椭圆C的方程为．
（2）设
，
，直线AB的方程为，
代入，得， 由△＞0，解得﹣4＜t＜4
由韦达定理得
，
．
∴
．
由此可得：四边形APBQ的面积
∴当t=0时，
．
名校课堂系列答案【题目】为调查银川市某校高中生是否愿意提供志愿者服务，用简单随机抽样方法从该校调查了50人，结果如下：
（1）用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人，其中男生抽取多少人？
（2）在（1）中抽取的6人中任选2人，求恰有一名女生的概率；
（3）你能否在犯错误的概率不超过0.010的前提下，认为该校高中生是否愿意提供志愿者服务与性别有关？
下面的临界值表供参考：
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
独立性检验统计量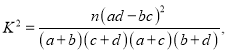
其中
【题目】某二手交易市场对某型号的二手汽车的使用年数
（
）与销售价格
（单位：万元/辆）进行整理，得到如下的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
（I）试求关于的回归直线方程
.
（参考公式：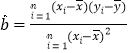
，
）
（II）已知每辆该型号汽车的收购价格为
万元，根据（I）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润
最大？（利润=销售价格-收购价格）
