题目内容
【题目】用数学归纳法证明命题“当n是正奇数时，xn＋yn能被x＋y整除”，在第二步的证明时，正确的证法是( )
A.假设n＝k(k∈N*)时命题成立，证明n＝k＋1时命题也成立
B.假设n＝k(k是正奇数)时命题成立，证明n＝k＋1时命题也成立
C.假设n＝k(k是正奇数)时命题成立，证明n＝k＋2时命题也成立
D.假设n＝2k＋1(k∈N)时命题成立，证明n＝k＋1时命题也成立
【答案】C
【解析】∵n为正奇数，当n＝k时，k下面第一个正奇数应为k＋2，而非k＋1.故应选C.
【考点精析】解答此题的关键在于理解数学归纳法的步骤的相关知识，掌握
- 步骤:A.命题在n=1（或
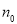）时成立，这是递推的基础；B.假设在n=k时命题成立； C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=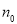,且
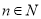)结论都成立
．
练习册系列答案
相关题目
