题目内容
【题目】已知函数f(x)=1+2sinxcosx+2cos2x.
(1)求f(x)递增区间;
(2)求f(x)的对称轴方程;
(3)求f(x)的最大值并写出取最大值时自变量x的集合.
【答案】
(1)解:函数f(x)=1+2sinxcosx+2cos2x=sin2x+cos2x+1= ![]() sin(2x+
sin(2x+ ![]() )+2.
)+2.
令 ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,解得
+2kπ,解得 ![]() ≤x≤
≤x≤ ![]() +kπ(k∈Z),
+kπ(k∈Z),
∴f(x)递增区间为[ ![]() ,
, ![]() +kπ](k∈Z)
+kπ](k∈Z)
(2)解:由2x+ ![]() =kπ+
=kπ+ ![]() ,解得x=
,解得x= ![]() +
+ ![]() (k∈Z),
(k∈Z),
∴f(x)的对称轴方程为:x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
(3)解:当2x+ ![]() =2kπ+
=2kπ+ ![]() ,解得x=kπ+
,解得x=kπ+ ![]() (k∈Z),f(x)max=
(k∈Z),f(x)max= ![]() +2.
+2.
∴f(x)取最大值时自变量x的集合为{x|x=kπ+ ![]() (k∈Z)}
(k∈Z)}
【解析】(1)利用倍角公式、和差公式可得函数f(x)= ![]() sin(2x+
sin(2x+ ![]() )+2.令
)+2.令 ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,解出即可得出f(x)递增区间.(2)由2x+
+2kπ,解出即可得出f(x)递增区间.(2)由2x+ ![]() =kπ+
=kπ+ ![]() ,解出x即可得出.(3)当2x+
,解出x即可得出.(3)当2x+ ![]() =2kπ+
=2kπ+ ![]() ,解得x=kπ+
,解得x=kπ+ ![]() (k∈Z),可得f(x)max=
(k∈Z),可得f(x)max= ![]() +2.
+2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知某产品的历史收益率的频率分布直方图如图所示:
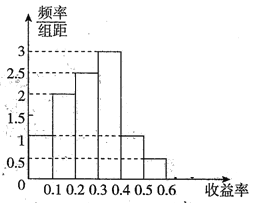
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.