题目内容
【题目】现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:现有1名女教师和2名男教师参加说题比赛,共有2道备选题目, 若每位选手从中有放回地随机选出一道题进行说题,
基本事件总数n=23=8,
设两道题分别为A,B题,
所以抽取情况共有:AAA,AAB,ABA,ABB,BAA,BAB,BBA,BBB,
其中第1个,第2个分别是两个女教师抽取的题目,第3个表示男教师抽取的题目,一共有8种;
其中满足恰有一男一女抽到同一题目的事件有:ABA,ABB,BAA,BAB,共4种,
故其中恰有一男一女抽到同一道题的概率为p= ![]() .
.
故选:C.
基本事件总数n=23=8,设两道题分别为A,B题,利用列举法求出满足恰有一男一女抽到同一题目的事件个数,由此能求出其中恰有一男一女抽到同一道题的概率.

练习册系列答案
相关题目
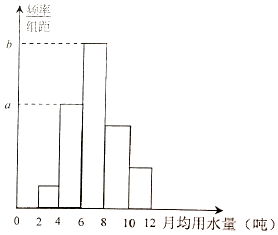
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组 | 频数 |
[2,4) | 2 |
[4,6) | 10 |
[6,8) | 16 |
[8,10) | 8 |
[10,12] | 4 |
合计 | 40 |
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率.