题目内容
(本小题满分12分)
已知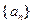 是各项都为正数的数列,其前
是各项都为正数的数列,其前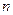 项和为
项和为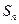 ,且满足
,且满足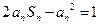 .
.
(Ⅰ)求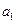 ,
,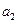 ,
,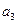 的值;
的值;
(Ⅱ)求数列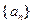 的通项公式;
的通项公式;
(Ⅲ)令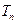 =
=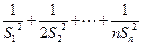 ,求证
,求证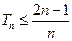 .
.
已知
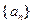 是各项都为正数的数列,其前
是各项都为正数的数列,其前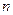 项和为
项和为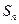 ,且满足
,且满足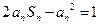 .
.(Ⅰ)求
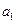 ,
,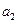 ,
,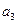 的值;
的值;(Ⅱ)求数列
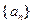 的通项公式;
的通项公式;(Ⅲ)令
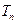 =
=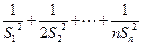 ,求证
,求证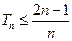 .
.(Ⅰ)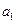 =1,
=1,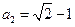 ,
,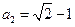
(Ⅱ)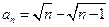
(Ⅲ)证明见解析。
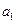 =1,
=1,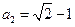 ,
,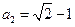
(Ⅱ)
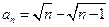
(Ⅲ)证明见解析。
(Ⅰ)解:(I)令
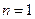 ,则有
,则有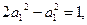
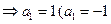 舍去).
舍去).令
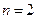 ,得
,得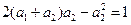 ,即
,即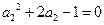 .
.∴
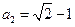 (舍去负值).
(舍去负值).同理,令
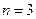 可解得
可解得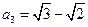 . 3分
. 3分(Ⅱ)解法一:(可猜想通项公式并用数学归纳法证明,略)
解法二:∵
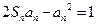 ,① 又
,① 又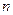 ≥2时有
≥2时有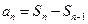 ,代入①式并整理得
,代入①式并整理得
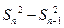 =1.∴
=1.∴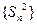 是首项为1,公差为1的等差数列. 6分
是首项为1,公差为1的等差数列. 6分∴
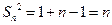 ,∴
,∴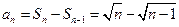 (
(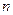 ≥2),又
≥2),又
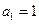
∴
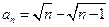 .
. 
 8分
8分(Ⅲ)由(Ⅱ)知
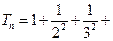 …+
…+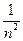 ≤1+
≤1+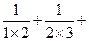 …
…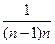
=1+1-
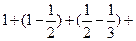 …+
…+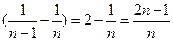 .
.即
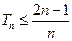 .
.  12分
12分
练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
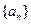 中,
中,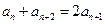 ,且
,且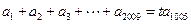 ,则
,则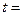
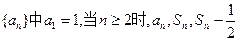 成等比数列。
成等比数列。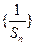 是等差数列;
是等差数列;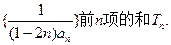
 满足:
满足: 且
且 ,则
,则 ______________.
______________.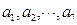 中,恰好有5个
中,恰好有5个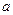 ,2个
,2个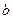
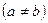 ,则不相同的数列共有 个.
,则不相同的数列共有 个. 为等差数列
为等差数列 的前n项和,
的前n项和, ,
,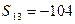 ,则
,则 与
与 的等比中项为( )
的等比中项为( )



 的前
的前 项和为
项和为 ,若
,若 则
则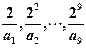 中最大的( )
中最大的( ) .
.
 .
.
 .
.
 .
.