题目内容
5.若{x|2x-a=0}⊆{x|-1<x<3},则实数a的取值范围是(-2,6).分析 根据题意,设A={x|2x-a=0},分析可得A={$\frac{a}{2}$},又由A⊆{x|-1<x<3},可得-1<$\frac{a}{2}$<3,解可得a的取值范围.
解答 解:根据题意,设A={x|2x-a=0},
则A={$\frac{a}{2}$},
若A⊆{x|-1<x<3},
必有-1<$\frac{a}{2}$<3,
解可得-2<a<6,即a的取值范围是(-2,6);
故答案为:(-2,6).
点评 本题考查集合的子集关系,关键分析集合{x|2x-a=0}的意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.在△ABC中,若b+c=$\sqrt{2}$+1,B=30°,C=45°,则( )
| A. | b=1,c=$\sqrt{2}$ | B. | b=$\sqrt{2}$,c=1 | C. | b=$\frac{\sqrt{2}}{2}$,c=1+$\frac{\sqrt{2}}{2}$ | D. | b=1+$\frac{\sqrt{2}}{2}$,c=$\frac{\sqrt{2}}{2}$ |
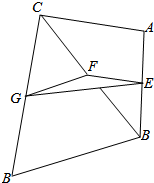 已知:AB、BC、CD是不在同一平面内的三条线段,E、F、G分别为AB、BC、CD的中点.求证.AC∥平面EFG,BD∥平面EFG.
已知:AB、BC、CD是不在同一平面内的三条线段,E、F、G分别为AB、BC、CD的中点.求证.AC∥平面EFG,BD∥平面EFG.