题目内容
【题目】已知曲线G上的点到点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小2.
的距离小2.
(1)求曲线G的方程.
(2)是否存在过F的直线l,使得l与曲线G相交于A,B两点,点A关于x轴的对称点为A',且△A'BF的面积等于4?若存在,求出此时直线l的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在;直线l的方程为
;(2)存在;直线l的方程为![]()
【解析】
(1)设S(x,y)为曲线G上任意一点,判断曲线G是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,求出曲线G的方程.
为准线的抛物线,求出曲线G的方程.
(2)设直线l的方程为![]() ,与抛物线C的方程联立,消去x,设
,与抛物线C的方程联立,消去x,设![]() ,通过韦达定理以及三角形的面积,转化求解m即可.
,通过韦达定理以及三角形的面积,转化求解m即可.
解:(1)设S(x,y)为曲线G上任意一点,
依题意,点S到![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等,
的距离相等,
所以曲线G是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
所以曲线G的方程为![]() .
.
(2)设直线l的方程为![]() ,与抛物线C的方程联立,
,与抛物线C的方程联立,
得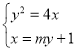 ,消去x,得
,消去x,得![]() ,
,
设![]() ,
,
则![]()
![]()
![]() ,
,
解得![]() ,
,
所以存在直线l使得△A'BF的面积等于4,此时直线l的方程为![]() .
.

练习册系列答案
相关题目