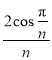题目内容
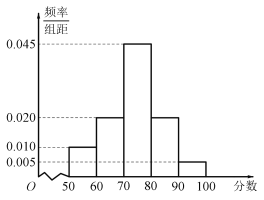
【题目】某校为了解该校学生“停课不停学”的网络学习效率，随机抽查了高一年级100位学生的某次数学成绩，得到如图所示的频率分布直方图：
（1）估计这100位学生的数学成绩的平均值
.（同一组中的数据用该组区间的中点值代表）；
（2）根据整个年级的数学成绩，可以认为学生的数学成绩
近似地服从正态分布
经计算，（1）问中样本标准差
的近似值为10．用样本平均数作为
的近似值，用样本标准差作为
的估计值，现任抽取一位学生，求他的数学成绩恰在64分到94分之间的概率.
参考数据:若随机变量
，则
，
，
（3）该年级1班的数学老师为了能每天督促学生的网络学习，提高学生每天的作业质量及学习数学的积极性，特意在微信上设计了一个每日作业小程序，每当学生提交的作业获得优秀时，就有机会参与一次小程序中“玩游戏，得奖励积分”的活动，开学后可根据获得积分的多少领取老师相应的小奖品.小程序页面上有一列方格，共15格，刚开始有只小兔子在第1格，每点一下游戏的开始按钮，小兔子就沿着方格跳一下，每次跳1格或跳2格，概率均为
，依次点击游戏的开始按钮，直到小兔子跳到第14格（奖励0分）或第15格（奖励5分）时，游戏结束，每天的积分自动累加，设小兔子跳到第
格的概率为
，试证明
是等比数列，并求
的值.（获胜的概率）
【答案】（1）74（2）0.8186（3）见解析，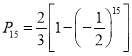
【解析】
（1）根据频率分布直方图直接结算即可；
（2）由
可知
，根据参考数据，即可得出
的概率；
（3）根据分类加法计数原理可知
，构造等比数列可得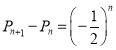
，
利用累加法求出
，即可求解.
（1）
（2）由，所以
，
.
（3）小兔子开始在第1格，为必然事件，
，
点一下开始按钮，小兔子跳1格即移到第2格的概率为
，即
，
小兔子移到第
格的情况是下列两种，而且也只有两种情况.
①小兔子先跳到第
格，又点一下开始按钮跳了2格，其概率为
；
②小兔了先跳到第
格，乂点一下开始按钮跳了1格，其概率为
；
因为，所以
.
所以当
时，
数列
是以
为首项，以
为公比的等比数列，
所以
，
.
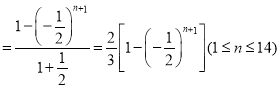所以获胜的概率.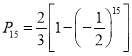
