题目内容
(本题满分14分)
如图,在平面直角坐标系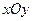 中,过
中,过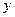 轴正方向上一点
轴正方向上一点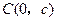 任作一直线,与抛物线
任作一直线,与抛物线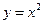 相交于
相交于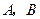 两点.一条垂直于
两点.一条垂直于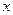 轴的直线,分别与线段
轴的直线,分别与线段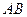 和直线
和直线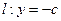 交于点
交于点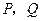 .
.
(1)若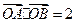 ,求
,求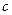 的值;(5分)
的值;(5分)
(2)若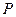 为线段
为线段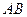 的中点,求证:
的中点,求证: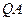 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)
(3)试问(2)的逆命题是否成立?说明理由.(4分)
如图,在平面直角坐标系
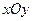 中,过
中,过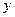 轴正方向上一点
轴正方向上一点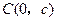 任作一直线,与抛物线
任作一直线,与抛物线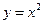 相交于
相交于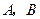 两点.一条垂直于
两点.一条垂直于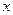 轴的直线,分别与线段
轴的直线,分别与线段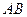 和直线
和直线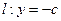 交于点
交于点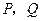 .
.(1)若
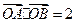 ,求
,求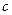 的值;(5分)
的值;(5分)(2)若
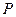 为线段
为线段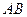 的中点,求证:
的中点,求证: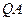 为此抛物线的切线;(5分)
为此抛物线的切线;(5分)(3)试问(2)的逆命题是否成立?说明理由.(4分)

(1)
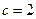
(2)
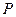 的横坐标为
的横坐标为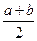 ,即
,即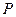 点是线段
点是线段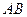 的中点
的中点(3)略
解:(1)设直线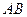 的方程为
的方程为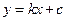 ,
,
将该方程代入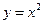 得
得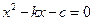 .
.
令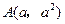 ,
,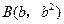 ,则
,则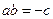 .
.
因为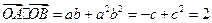 ,解得
,解得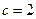 ,
,
或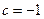 (舍去).故
(舍去).故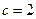 .
.
(2)由题意知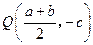 ,直线
,直线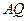 的斜率为
的斜率为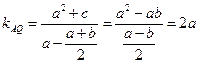 .
.
又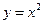 的导数为
的导数为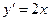 ,所以点
,所以点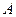 处切线的斜率为
处切线的斜率为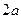 ,
,
因此,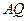 为该抛物线的切线.
为该抛物线的切线.
(3)(2)的逆命题成立,证明如下:
设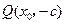 .
.
若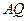 为
为 该抛物线的切线,则
该抛物线的切线,则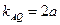 ,
,
又直线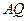 的斜率为
的斜率为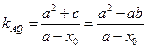 ,所以
,所以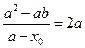 ,
,
得 ,因
,因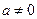 ,有
,有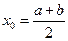 .
.
故点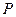 的横坐标为
的横坐标为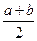 ,即
,即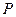 点是线段
点是线段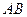 的中点.
的中点.
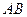 的方程为
的方程为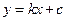 ,
,将该方程代入
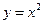 得
得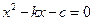 .
.令
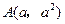 ,
,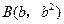 ,则
,则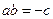 .
.因为
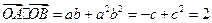 ,解得
,解得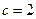 ,
,或
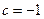 (舍去).故
(舍去).故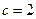 .
.(2)由题意知
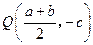 ,直线
,直线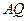 的斜率为
的斜率为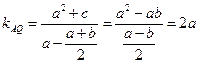 .
.又
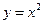 的导数为
的导数为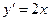 ,所以点
,所以点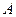 处切线的斜率为
处切线的斜率为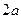 ,
,因此,
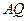 为该抛物线的切线.
为该抛物线的切线.(3)(2)的逆命题成立,证明如下:
设
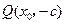 .
.若
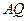 为
为 该抛物线的切线,则
该抛物线的切线,则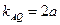 ,
,又直线
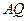 的斜率为
的斜率为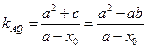 ,所以
,所以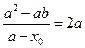 ,
,得
 ,因
,因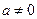 ,有
,有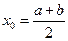 .
.故点
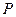 的横坐标为
的横坐标为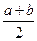 ,即
,即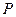 点是线段
点是线段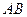 的中点.
的中点.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
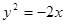
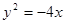
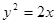
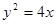
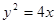 的焦点作直线与抛物线交于
的焦点作直线与抛物线交于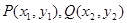 两点,若
两点,若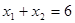 ,则
,则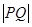 的值为
的值为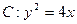 的准线与
的准线与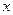 轴交于
轴交于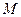 点,
点,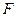 为抛物线
为抛物线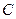 的焦点,过
的焦点,过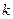 的直线与抛物线
的直线与抛物线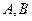 两点。
两点。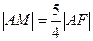 ,求
,求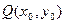 满足
满足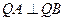 ,若存在,求
,若存在,求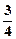 m,则水面上涨到与抛物线拱顶相距
m,则水面上涨到与抛物线拱顶相距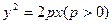 的焦点
的焦点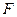 的直线
的直线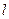 交抛物线于点
交抛物线于点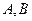 ,交其准线于点
,交其准线于点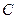 ,若
,若 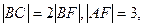 则此抛物线的方程为 ( )
则此抛物线的方程为 ( )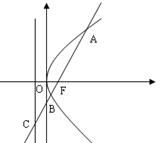
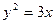
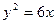

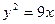

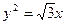
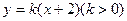 与抛物线
与抛物线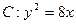 相交于
相交于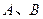 两点,
两点,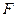 为
为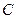 的焦点,若
的焦点,若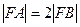 ,则
,则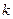 等于( )
等于( )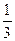
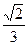


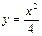 的焦点坐标是( )
的焦点坐标是( )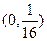
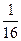 ,0)
,0)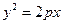 的焦点与椭圆
的焦点与椭圆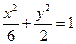 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )