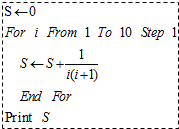题目内容
6.已知函数f(x)=mlnx-$\frac{1}{2}$x2(m∈R)满足f'(1)=1.(1)求m的值及函数f(x)的单调区间;
(2)若函数g(x)=f(x)-($\frac{1}{2}$x2-3x+c)在[1,3]内有两个零点,求实数c的取值范围.
分析 (1)求出函数的定义域,求出函数的导数,利用函数的导数的符号判断函数的单调性,求出单调区间.
(2)推出g(x)=2lnx-x2+3x-c,求出函数的导数判断好的单调性,利用函数g(x)在[1,3]有两个零点列出不等式组,然后求出c的范围.
解答 (本小题满分14分)
解:(1)函数$f(x)=mlnx-\frac{1}{2}{x^2}$的定义域是(0,+∞). …(1分)
∵${f}^{′}(x)=\frac{m}{x}-$x,由f′(1)=1得m-1=1,
∴m=2,即$f′(x)=\frac{2}{x}-x=\frac{2-{x}^{2}}{x}$ …(2分)
令f′(x)=0得:$x=\sqrt{2}$或$x=-\sqrt{2}$(舍去). …(3分)
当$x∈(0,\sqrt{2})$时,f′(x)>0,∴f(x)在$(0,\sqrt{2})$上是增函数;
当$x∈(\sqrt{2},+∞)$时,f′(x)<0,∴f(x)在$(\sqrt{2},+∞)$上是减函数.…(5分)
∴函数f(x)的增区间是$(0,\sqrt{2})$,减区间是$(\sqrt{2},+∞)$.…(6分)
(2)由(1)可知$f(x)=2lnx-\frac{1}{2}{x^2}$,
∴g(x)=2lnx-x2+3x-c,…(7分)
∴$g′(x)=\frac{2}{x}-2x+3=\frac{-2{x}^{2}+3x+2}{x}$.…(8分)
令g′(x)=0得:x=2或$x=-\frac{1}{2}$(舍去).…(9分)
当x∈[1,2)时,g′(x)>0,则g(x)在[1,2)上单调递增;
当x∈(2,3]时,g′(x)<0,则g(x)在(2,3]上单调递减.…(10分)
又∵函数g(x)在[1,3]有两个零点等价于:$\left\{\begin{array}{l}g(1)≤0\\ g(2)>0\\ g(3)≤0\end{array}\right.$,…(12分)
∴$\left\{\begin{array}{l}2-c≤0\\ 2ln2+2-c>0\\ 2ln3-c≤0\end{array}\right.$$⇒\left\{\begin{array}{l}c≥2\\ c<2ln2+2\\ c≥2ln3\end{array}\right.⇒2ln3≤c<2ln2+2$,…(13分)
∴实数c的取值范围是$[2ln3,_{\;}^{\;}2ln2+2)$. …(14分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值,函数的零点的求法考查分析问题解决问题的能力,转化思想的应用.

| A. | {2,4,5} | B. | {1,3,5} | C. | {2,4} | D. | {1,2,3,4,5} |
| A. | -2 | B. | -3 | C. | -4 | D. | -2$\sqrt{3}$ |
| A. | 6:3:2 | B. | 3:2:6 | C. | 2:6:3 | D. | 6:2:3 |
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |