题目内容
11.如图是一个算法的伪代码,其输出的结果为$\frac{10}{11}$.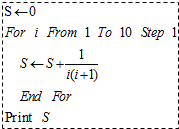
分析 模拟执行伪代码,可得伪代码的功能是计算并输出S=0+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{10×11}$的值,从而得解.
解答 解:模拟执行伪代码,可得:S=0+$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{10×11}$=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+…+($\frac{1}{10}$-$\frac{1}{11}$)=1-$\frac{1}{11}$=$\frac{10}{11}$.
故答案为:$\frac{10}{11}$.
点评 本题主要考查了循环结构的程序框图,属于基本知识的考查.

练习册系列答案
相关题目
1.双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若F关于直线y=$\sqrt{3}$x的对称点P在双曲线上,则C的离心率为( )
| A. | 2 | B. | $\frac{\sqrt{5}+1}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{3}$+1 |
1.下表给出一个等比数阵
其中每行每列都是等比数列,aij
表示第i行第j列的数.
(1)写出a34的值并求出aij的计算公式;
(2)若数列{bn}满足bn=a2n+log2a2n,求数列{bn}的前n项和Sn.
| 1 | 2 | ( ) | ( ) | ( ) | … | a1j | … |
| 3 | 6 | ( ) | ( ) | ( ) | … | a2j | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | … | … |
表示第i行第j列的数.
(1)写出a34的值并求出aij的计算公式;
(2)若数列{bn}满足bn=a2n+log2a2n,求数列{bn}的前n项和Sn.