题目内容
【题目】已知动点![]() 在
在![]() 轴上方,且到定点
轴上方,且到定点![]() 距离比到
距离比到![]() 轴的距离大
轴的距离大![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() ,
,![]() 分别异于原点
分别异于原点![]() ,在曲线
,在曲线![]() 的
的![]() ,
,![]() 两点处的切线分别为
两点处的切线分别为![]() ,
,![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 在定直线上.
在定直线上.
【答案】(1)![]()
![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)设![]()
![]() ,由到定点
,由到定点![]() 距离比到
距离比到![]() 轴的距离大
轴的距离大![]() ,可得
,可得![]() ,化简可得点
,化简可得点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)由题意可知,直线![]() 的斜率存在且不为
的斜率存在且不为![]() ,设直线
,设直线![]() 的方程为
的方程为![]()
![]() 与
与![]() 联立,设
联立,设![]() ,
,![]() ,可得
,可得![]() ,
,![]() 的值,又
的值,又![]() ,所以
,所以![]() ,可得切线
,可得切线![]() 的方程,同理可得切线
的方程,同理可得切线![]() 的方程,求出交点坐标,可得其在定直线上.
的方程,求出交点坐标,可得其在定直线上.
解:(1)设![]()
![]() ,
,
则有![]() ,化简得
,化简得![]()
![]() ,
,
故轨迹![]() 的方程为
的方程为![]()
![]() .
.
(2)由题意可知,直线![]() 的斜率存在且不为
的斜率存在且不为![]() ,
,
设直线![]() 的方程为
的方程为![]()
![]() 与
与![]()
联立得![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以切线![]() 的方程为
的方程为![]() ,
,
即![]() ,
,
同理切线![]() 的方程为
的方程为![]()
联立得![]() ,
,![]() .
.
两式消去![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以交点![]() 的轨迹为直线
的轨迹为直线![]() ,去掉
,去掉![]() 点.
点.
因而交点![]() 在定直线上.
在定直线上.

练习册系列答案
相关题目
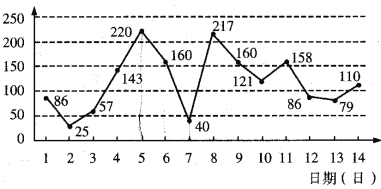
【题目】下图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
空气质量指数 | 污染程度 |
小于100 | 优良 |
大于100且小于150 | 轻度 |
大于150且小于200 | 中度 |
大于200且小于300 | 重度 |
(1)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(2)求此人到达当日空气质量优良的概率;
(3)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
