Question

【题目】已知函数的图象与直线相切，是的导函数，且.

（1）求；

（2）函数的图象与曲线关于轴对称，若直线与函数的图象有两个不同的交点，求证：.

Answer 1

【答案】（1）（2）证明见解析

【解析】

（1）设直线与函数的图象相切的切点为，求得的导数可得切线的斜率，由切线方程和已知条件，可得方程组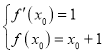与可解得，进而得到所求的解析式；

（2）求得的解析式,，，两式相加和相减，相除可得,令，可得要证，即证，即证，可令求得二阶导数,判断单调性,即可得证．

假设直线与函数图象的切点为，

因为，

则由题意知，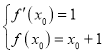

即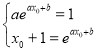

所以，即①，

又，所以②

由①②可得，所以

（2）由题可知，

则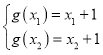，即，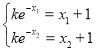

两式相加得，

两式相减得，

以上两式相除得，

即，

不妨设，

要证，即证，

即，

即证，

令，

那么，则，

所以在上递增，又，

所以当时，恒成立，

所以在上递增，且.

所以，

从而成立.