题目内容

7．设z=3x+y，实数x，y满足$\left\{\begin{array}{l}{2x+y≥0}\\{2x-y≤0}\\{0≤y≤t}\end{array}\right.$，其中t＞0，若z的最大值为5，则实数t的值为2．

分析 由题意作出其平面区域，将z=3x+y化为y=-3x+z，z相当于直线y=-3x+z的纵截距，从而解方程组$\left\{\begin{array}{l}{y=-3x+5}\\{y=2x}\end{array}\right.$，求出t的值即可．

解答 解：由题意作出其平面区域，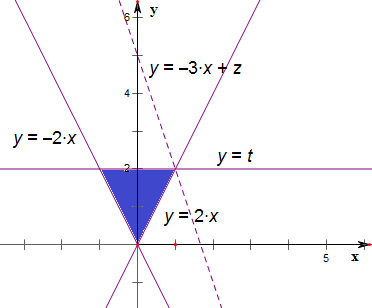

将z=3x+y化为y=-3x+z，z相当于直线y=-3x+z的纵截距，
故结合图象可得，
解$\left\{\begin{array}{l}{y=-3x+5}\\{y=2x}\end{array}\right.$，得：x=1，y=2；
故t=2，
故答案为：2．

点评 本题考查了简单线性规划，作图要细致认真，属于中档题．

练习册系列答案
相关题目
17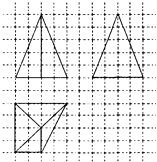．如图，网格纸上小止方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的体积为（　　）
A．16B．20C．4$\sqrt{29}$D．60
18．直角三角形ABC中，A为直角，AB=13，AC=3，P、Q为△ABC所在平面内的点，满足$\overrightarrow{AB}$=-2$\overrightarrow{AC}$+3$\overrightarrow{AP}$，$\overrightarrow{CA}$+$\overrightarrow{CB}$=2$\overrightarrow{CQ}$，则$\overrightarrow{AP}$在$\overrightarrow{CQ}$方向上的投影为$\frac{133\sqrt{205}}{615}$．
15．已知等差数列{an}的前n项和为Sn，且满足：a2+a4=14，S7=70．
（1）求数列{an}的通项公式；
（2）设Tn=2Sn-7n，求Tn的最小值．
2．已知定义域为R的函数f（x）=$\frac{2a+2bx+sinx+（a+bx）cosx}{2+cosx}$（a，b∈R）有最大值和最小值，且最大值与最小值的和为8，则2a-3b=（　　）
A．7B．8C．9D．1
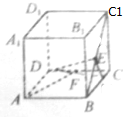12．如图，在正方体ABCD-A1B1C1D1中，E、F分别是BC1，DC的中点．
（1）求直线DE与平面ABCD所成角的正切值；
（2）求证：AF⊥DE．
19．函数y=3sin（4x+$\frac{π}{3}$）-3的最小正周期为$\frac{π}{2}$，单调递减区间为[$\frac{kπ}{2}$+$\frac{π}{24}$，$\frac{kπ}{2}$+$\frac{7π}{24}$]，k∈z．
16．集合A={x|x+1≥5}，B={y|y=x2+2x+5，x∈R}，则A、B表示（表示/不表示）同一集合．
14．?ABCD中，OA=4，OC=2，|$\overrightarrow{OB}$|=2$\sqrt{7}$，M为OA的中点，P为线段BC上一动点（包括端点）．
（1）求∠ABC；
（2）是否存在实数λ，使（λ$\overrightarrow{OA}$-$\overrightarrow{OP}$）⊥$\overrightarrow{CM}$？若存在，求出满足条件的实数λ的取值范围，不存在请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网