题目内容
4.已知圆锥底面半径与球的半径都是1cm,如果圆锥的体积与球的体积恰好也相等,那么这个圆锥的侧面积是$\sqrt{17}$πcm2.分析 由已知求出圆锥的母线长,代入圆锥的侧面积公式,可得答案.
解答 解:由题意可知球的体积为:$\frac{4π}{3}$×13=$\frac{4π}{3}$cm3,
圆锥的体积为:$\frac{1}{3}$×π×12×h=$\frac{π}{3}$hcm3,
因为圆锥的体积恰好也与球的体积相等,
所以 $\frac{4π}{3}$=$\frac{π}{3}$h,所以h=4cm,
圆锥的母线:l=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$cm.
故圆锥的侧面积S=πrl=$\sqrt{17}$πcm2,
故答案为:$\sqrt{17}$π
点评 本题考查球的体积与圆锥的体积公式的应用,考查计算能力.

练习册系列答案
相关题目
9.“a+b>0”是“任意的x∈[0,1],ax+b>0恒成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
10.若一个函数存在定义域和值域相同的区间,则称这个函数为这个区间上的一个“保城函数”,给出下列四个函数:
①f(x)=-x3;
②f(x)=3x;
③f(x)=sin$\frac{πx}{3}$;
④f(x)=2ln3x-3.
其中可以找到一个区间使其为保城函数的有( )
①f(x)=-x3;
②f(x)=3x;
③f(x)=sin$\frac{πx}{3}$;
④f(x)=2ln3x-3.
其中可以找到一个区间使其为保城函数的有( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
11.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{b}$|=4,($\overrightarrow{a}$-$\overrightarrow{c}$)•($\overrightarrow{b}$-$\overrightarrow{c}$)=0,若对每一个确定的$\overrightarrow b$,|$\overrightarrow{c}$|的最大值和最小值分别为m,n,则m-n的值为( )
| A. | 随$|\overrightarrow a|$增大而增大 | B. | 随$|\overrightarrow a|$增大而减小 | C. | 是2 | D. | 是4 |
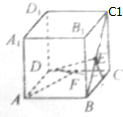 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.