题目内容
已知实数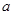 满足
满足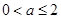 ,
,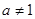 ,设函数
,设函数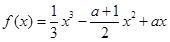
(1)当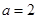 时,求
时,求 的极小值;
的极小值;
(2)若函数 (
(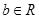 )的极小值点与
)的极小值点与 的极小值点相同,求证:
的极小值点相同,求证: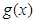 的极大值小于等于
的极大值小于等于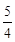
(1)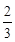 ;(2)见解析
;(2)见解析
解析试题分析:(1)把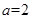 代入原函数先得解析式,再求导数,列表判断单调性求函数的极小值;(2)先分别求函数
代入原函数先得解析式,再求导数,列表判断单调性求函数的极小值;(2)先分别求函数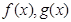 的导函数,再分
的导函数,再分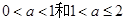 两种情况讨论,根据条件函数
两种情况讨论,根据条件函数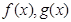 的极小值点相同分别求
的极小值点相同分别求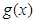 的极大值,从而进行判断得结论
的极大值,从而进行判断得结论
试题解析:(Ⅰ) 解: 当a=2时,f ′(x)=x2-3x+2=(x-1)(x-2)
列表如下:x (- 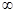 ,1
,1 )
)1 (1,2) 2 (2,+ 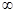 )
)f ′(x) + 0 - 0 + f (x) 单调递增 极大值 单调递减 极小值 单调递增
所以,f (x)极小值为f (2)=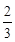 5分
5分
(Ⅱ) 解:f ′(x)=x2-(a+1)x+a=(x-1)(x-a)
g ′(x)=3x2+2bx-(2b+4)+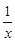 =
=
令p(x)=3x2+(2b+3)x-1,
(1)当 1<a≤2时,
f(x)的极小值点x=a,则g(x)的极小值点也为x=a,
所以pA=0,
即3a2+(2b+3)a-1=0,
即b=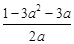 ,
,
此时g(x)极大值=g(1)=1+b-(2b+4)=-3-b
=-3+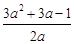 =
=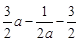
由于1<a≤2,
故 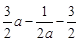 ≤
≤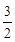
 2-
2-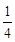 -
-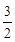 =
=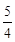 10分
10分
(2)当0<a<1时,
f(x)的极小值点x=1,则g(x)的极小值点为x=1,
由于p(x)=0有一正一负两实根,不妨设x2<0<x1,
所以0<x1<1,
即p(1)=3+2b+3-1>0,
故b>-
此时g(x)的极大值点x=x1,
有 g(x1)=x13+bx12-(2b+4)x1+lnx1
<1+bx12-(2b+4)x1
=(x12-2x1)b-4x1+1 (x12-2x1<0)
<- (x12-2x1)-4x1+1
(x12-2x1)-4x1+1
=- x12+x1+1
x12+x1+1
=- (x1-
(x1-

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案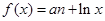 ,其中实数a为常数.
,其中实数a为常数. 的单调区间:
的单调区间: (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值; .
. 元,则销售量
元,则销售量 (单位:件)与零售价
(单位:件)与零售价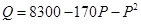 ,问该商品零售价定为多少元时毛利润
,问该商品零售价定为多少元时毛利润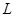 最大,并求出最大毛利润.(毛利润
最大,并求出最大毛利润.(毛利润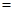 销售收入
销售收入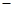 进货支出)
进货支出) .
. 的单调递减区间;
的单调递减区间;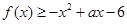 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围; 作函数
作函数 图像的切线,求切线方程
图像的切线,求切线方程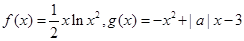 。
。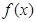 在
在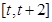
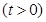 上的最小值;
上的最小值;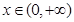 ,
,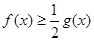 恒成立,求实数
恒成立,求实数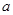 的取值范围.
的取值范围.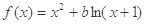 ,其中
,其中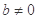 .
.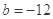 ,求
,求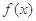 在
在 的最小值;
的最小值;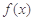 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数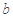 的取值范围;
的取值范围;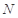 ,使得当
,使得当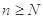 时,不等式
时,不等式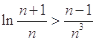 恒成立.
恒成立.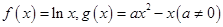 .
. 与
与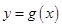 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数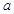 的值及点P的坐标;
的值及点P的坐标; 在
在 处的切线与
处的切线与 轴平行.
轴平行. 的值和函数
的值和函数 的单调区间;
的单调区间; 的图象与抛物线
的图象与抛物线 恰有三个不同交点,求
恰有三个不同交点,求 的取值范围.
的取值范围.
 单调递增区间;
单调递增区间; ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围.