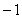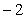题目内容
已知奇函数f(x)和偶函数g(x)的定义域都是(-∞,0)∪(0,+∞),且当x<0时,f’(x)g(x)+f(x)g’(x)>0.若g(-2)=0,则不等式f(x)g(x)>0的解集是______.
由题意,∵奇函数f(x)和偶函数g(x)
∴f(x)g(x)是奇函数
∵当x<0时,f’(x)g(x)+f(x)g’(x)>0
∴当x<0时,f(x)g(x)是增函数
∴当x>0时,f(x)g(x)是增函数
∵g(-2)=g(2)=0
∴不等式f(x)g(x)>0的解集是(-2,0)∪(2,+∞)
故答案为(-2,0)∪(2,+∞)
∴f(x)g(x)是奇函数
∵当x<0时,f’(x)g(x)+f(x)g’(x)>0
∴当x<0时,f(x)g(x)是增函数
∴当x>0时,f(x)g(x)是增函数
∵g(-2)=g(2)=0
∴不等式f(x)g(x)>0的解集是(-2,0)∪(2,+∞)
故答案为(-2,0)∪(2,+∞)

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
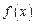 是
是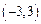 上的奇函数,当
上的奇函数,当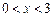 时,
时,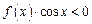 的解集是( )
的解集是( )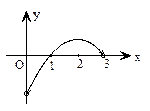
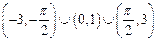
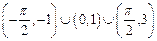
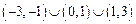
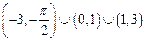
 ,
,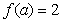 ,则
,则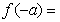 ( )
( )