题目内容
若(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,则实数m的取值范围是( )
| A.m>1 | B.m<-1 | ||||
C.m<-
| D.m>1或m<-
|
∵(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,
①当m+1=0,即m=-1时,不等式为x<0,不符合题意;
②当m+1≠0,即m≠-1时,由(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,
∴
,解得m<-‘
,
∴实数m的取值范围是m<-‘
.
故选C.
①当m+1=0,即m=-1时,不等式为x<0,不符合题意;
②当m+1≠0,即m≠-1时,由(m+1)x2-(m-1)x+3(m-1)<0对任意实数x恒成立,
∴
|
| 13 |
| 11 |
∴实数m的取值范围是m<-‘
| 13 |
| 11 |
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
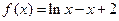 的零点个数为 .
的零点个数为 . 