题目内容
15.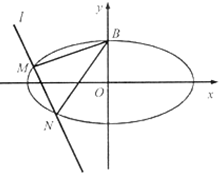 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点B(0,1)在椭圆C上,且△BF1F2的周长为4+2$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点B(0,1)在椭圆C上,且△BF1F2的周长为4+2$\sqrt{3}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)若斜率为k的直线l与椭圆C交于M,N两点,且满足直线BM与直线BN的斜率之积为$\frac{1}{2}$.试用k表示△BMN面积S,并求S的最大值.
分析 (I)由题意可知:$\left\{\begin{array}{l}{b=1}\\{2a+2c=4+2\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得即可得出椭圆C的方程;
(II)设MN:y=kx+m,M(x1,y1),N(x2,y2),与椭圆方程联立化为(1+4k2)x2+8kmx+4m2-4=0,△>0.由kBM•kBN=$\frac{{y}_{1}-1}{{x}_{1}}•\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{1}{2}$,利用根与系数的关系代入化简可得:m2+2m-3=0,解得m.再利用|MN|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,点B到直线MN的距离d=$\frac{4}{\sqrt{1+{k}^{2}}}$,可得S△BMN=$\frac{1}{2}|MN|•d$,通过换元利用基本不等式的性质即可得出.
解答 解:(I)由题意可知:$\left\{\begin{array}{l}{b=1}\\{2a+2c=4+2\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,c=$\sqrt{3}$.
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(II)设MN:y=kx+m,M(x1,y1),N(x2,y2),联立$\left\{\begin{array}{l}{{x}^{2}+4{y}^{2}=4}\\{y=kx+m}\end{array}\right.$,化为(1+4k2)x2+8kmx+4m2-4=0,
△=16(4k2-m2+1)>0,
∴x1+x2=$\frac{-8km}{1+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$,
∵kBM•kBN=$\frac{{y}_{1}-1}{{x}_{1}}•\frac{{y}_{2}-1}{{x}_{2}}$=$\frac{{k}^{2}{x}_{1}{x}_{2}+k(m-1)({x}_{1}+{x}_{2})+(m-1)^{2}}{{x}_{1}{x}_{2}}$=$\frac{1}{2}$,
∴$({k}^{2}-\frac{1}{2})$x1x2+k(m-1)(x1+x2)+(m-1)2=0,
∴$({k}^{2}-\frac{1}{2})$$•\frac{4{m}^{2}-4}{1+4{k}^{2}}$+$k(m-1)×\frac{-8km}{1+4{k}^{2}}$+(m-1)2=0,
化为m2+2m-3=0,解得m=-3或m=1(舍去).
∴|MN|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}×\frac{4\sqrt{4{k}^{2}+1-{m}^{2}}}{1+4{k}^{2}}$=$\frac{8\sqrt{1+{k}^{2}}\sqrt{{k}^{2}-2}}{1+4{k}^{2}}$.
点B到直线MN的距离d=$\frac{4}{\sqrt{1+{k}^{2}}}$,
∴S△BMN=$\frac{1}{2}|MN|•d$=$\frac{16\sqrt{{k}^{2}-2}}{1+4{k}^{2}}$,
由m=-3,△>0,可知:k2-2>0,令$\sqrt{{k}^{2}-2}$=t>0,
∴k2=t2+2,
∴S=$\frac{16t}{4{t}^{2}+9}$=$\frac{16}{4t+\frac{9}{t}}$$≤\frac{4}{3}$,当且仅当t=$\frac{3}{2}$,
即k=$±\frac{\sqrt{17}}{2}$时,Smax=$\frac{4}{3}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、斜率计算公式、点到直线的距离公式、三角形面积计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | 2或2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
 在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
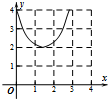
在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.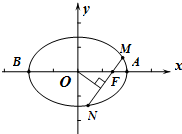 如图:已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆,A,B为顶点,过右焦点的弦MN的长度为y,中心O到弦MN的距离为d,点M从右顶点A开始按逆时针方向在椭圆上移动到B停止,当0°≤∠MFA≤90°时,记x=d,当90°<∠MFA≤180°,记x=2$\sqrt{2}$-d,函数y=f(x)图象是( )
如图:已知方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1的椭圆,A,B为顶点,过右焦点的弦MN的长度为y,中心O到弦MN的距离为d,点M从右顶点A开始按逆时针方向在椭圆上移动到B停止,当0°≤∠MFA≤90°时,记x=d,当90°<∠MFA≤180°,记x=2$\sqrt{2}$-d,函数y=f(x)图象是( )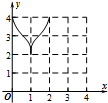

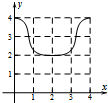
 绵阳二诊后,某学校随机抽査部分学生的政治成绩进行统计分析,己知统计出的成绩频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100),己知低于60 分的人数是6人.
绵阳二诊后,某学校随机抽査部分学生的政治成绩进行统计分析,己知统计出的成绩频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100),己知低于60 分的人数是6人.