题目内容
3. 在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.
在棱锥A-BCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,F是BC的中点,AB=AC=BE=2,CD=1.(1)求证:EF⊥AD;
(2)求三棱锥F-ADE的高.
分析 (1)利用线面垂直的判定与性质证明AF⊥FE,利用勾股定理,证明DF⊥EF,可得EF⊥平面AFD,即可证明FE⊥A
D;
(2)利用等体积法求三棱锥F-ADE的高.
解答 (1)证明:∵DC⊥平面ABC,∴DC⊥AF,
又∵AB=AC,F是BC的中点,∴AF⊥BC,
∴AF⊥平面BCD
∴AF⊥FE…2分
在△DEF中,DE2=BC2+(EB-DC)2=9,DF2=DC2+CF2=3,EF2=EB2+BF2=6,
∴DE2=DF2+EF2,∴DF⊥EF,…5分
∴EF⊥平面AFD,故FE⊥AD…6分
(2)解:由(1)知DF⊥EF,∴S△DEF=$\frac{1}{2}$DF×EF=$\frac{1}{2}\sqrt{3}×\sqrt{6}=\frac{{3\sqrt{2}}}{2}$…7分
∵S△DEF=S梯形BCDE-S△DCF-S△BEF=$\frac{1}{2}(2\sqrt{2}×3-\sqrt{2}×1-\sqrt{2}×2)=\frac{3}{2}\sqrt{2}$…7分)
在△DEF中,$AD=\sqrt{5},DE=3,AE=2\sqrt{2}$
∴由余弦定理得$cos∠ADE=\frac{9+5-8}{{2×3\sqrt{5}}}=\frac{1}{{\sqrt{5}}}$,∴$sin∠ADE=\frac{2}{{\sqrt{5}}}$…9分
∴S△DEA=$\frac{1}{2}×3×\sqrt{5}×\frac{2}{{\sqrt{5}}}=3$
设三棱锥F-ADE的高h,则$\frac{1}{3}$S△DEF×AF=$\frac{1}{3}×\frac{3}{2}\sqrt{2}×\sqrt{2}=\frac{1}{3}×3h$
∴h=1,即三棱锥F-ADE的高为1…12分.
点评 证明线线垂直通常利用线面垂直进行证明,求三棱锥的高可利用等体积法进行转化求解.

| A. | $\sqrt{3}$-1 | B. | $\sqrt{2}$-1 | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
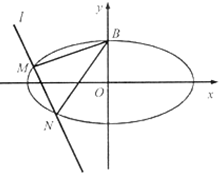 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点B(0,1)在椭圆C上,且△BF1F2的周长为4+2$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点为F1,F2,点B(0,1)在椭圆C上,且△BF1F2的周长为4+2$\sqrt{3}$.