题目内容
5．已知圆M：x2+y2+2mx-3=0（m＜0）的半径为2，则椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1（a＞0）的左焦点为F（-x，0），若垂直于x轴且经过F点的直线l与圆M相切，则a的值为（ ）| A． | 2或2$\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | 2 | D． | 4 |
分析 先把圆的方程整理成标准方程，根据半径求得m的值，进而根据题意求得F的坐标，最后利用椭圆的简单性质求得a．
解答 解：整理圆M的方程得（x+m）2+y2=m2+3，
∴m2+3=4，m=±1，
∵m＜0，
∴m=-1，
∴圆M的圆心为（1，0）半径为2，
∴左焦点F的坐标为（-1，0），
∴a2-3=1，
a=±2，
∵a＞0，
∴a=2，
故选：C．
点评 本题主要考查了直线与圆的方程的应用，椭圆的简单性质的运用．注重了对学生基础知识的考查．
练习册系列答案
名校联盟快乐课堂系列答案
相关题目
17．某工厂有工人500名，记35岁以上（含35岁）的为A类工人，不足35岁的为B类工人，为调查该厂工人的个人文化素质状况，现用分层抽样的方法从A、B两类工人中分别抽取了40人、60人进行测试．
（I）求该工厂A、B两类工人各有多少人？
（Ⅱ）经过测试，得到以下三个数据图表：（茎、叶分别是十位和个位上的数字）（如图）
表：100名参加测试工人成绩频率分布表
①先填写频率分布表中的六个空格，然后将频率分布直方图（图二）补充完整；
②该厂拟定从参加考试的79分以上（含79分）的B类工人中随机抽取2人参加高级技工培训班，求抽到的2人分数都在80分以上的概率．
（I）求该工厂A、B两类工人各有多少人？
（Ⅱ）经过测试，得到以下三个数据图表：（茎、叶分别是十位和个位上的数字）（如图）
表：100名参加测试工人成绩频率分布表
| 组号 | 分组 | 频数 | 频率 |
| 1 | [55，60） | 5 | 0.05 |
| 2 | [60，65） | 20 | 0.20 |
| 3 | [65，70） | ||
| 4 | [70，75） | 35 | 0.35 |
| 5 | [75，80） | ||
| 6 | [80，85） | ||
| 合计 | 100 | 1.00 | |
②该厂拟定从参加考试的79分以上（含79分）的B类工人中随机抽取2人参加高级技工培训班，求抽到的2人分数都在80分以上的概率．
18．实数x，y满足：-4≤x-y≤-1，-1≤4x-y≤5，则9x-y的取值范围是（ ）
| A． | [-7，26] | B． | [-1，20] | C． | [4，15] | D． | [1，15] |
17．从椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上一点P向x轴作垂线，垂足恰为右焦点F2，A是椭圆与x轴负半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP（O是坐标原点），则该椭圆的离心率是（ ）
| A． | $\frac{{\sqrt{2}}}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
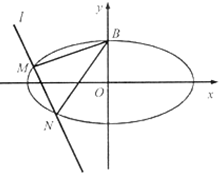已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点为F1，F2，点B（0，1）在椭圆C上，且△BF1F2的周长为4+2$\sqrt{3}$．