题目内容
【题目】已知等差数列![]() 的公差d>0,则下列四个命题:
的公差d>0,则下列四个命题:
①数列![]() 是递增数列; ②数列
是递增数列; ②数列![]() 是递增数列;
是递增数列;
③数列![]() 是递增数列; ④数列
是递增数列; ④数列![]() 是递增数列.
是递增数列.
其中正确命题的个数为( )
A.1B.2C.3D.4
【答案】B
【解析】
根据等差数列的通项公式和前![]() 项和公式,结合数列的通项公式的函数性质进行求解即可.
项和公式,结合数列的通项公式的函数性质进行求解即可.
①:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
因此可以把![]() 看成关于
看成关于![]() 的一次函数,
的一次函数,
而![]() ,所以数列
,所以数列![]() 是递增数列,因此本命题是真命题;
是递增数列,因此本命题是真命题;
②:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
因此可以把![]() 看成关于
看成关于![]() 的二次函数,而二次函数的单调性与开口和对称轴有关,
的二次函数,而二次函数的单调性与开口和对称轴有关,
虽然![]() 能确定开口方向,但是不能确定对称轴的位置,故不能判断数列
能确定开口方向,但是不能确定对称轴的位置,故不能判断数列![]() 的单调性,故本命题是假命题;
的单调性,故本命题是假命题;
③:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
设![]() ,因此数列
,因此数列![]() 的通项公式为:
的通项公式为:![]() ,
,
显然当![]() 时,数列
时,数列![]() 是常数列,故本命题是假命题;
是常数列,故本命题是假命题;
④:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
设![]() ,因此数列
,因此数列![]() 的通项公式为
的通项公式为![]() ,
,
所以可以把![]() 看成关于
看成关于![]() 的一次函数,
的一次函数,
而![]() ,所以数列
,所以数列![]() 是递增数列,因此本命题是真命题.
是递增数列,因此本命题是真命题.
故选:B

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 | |||||||||
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 | |||||||||
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | ||||||||||
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 | |||||||||
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 求 |
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(1)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该社区在2019年在“文化丹青”上的投资金额.
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为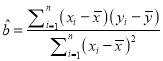 ,
, ![]() .)
.)