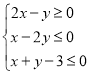Question

【题目】已知双曲线C1：-=1．

（1）若点M（3，t）在双曲线C1上，求M点到双曲线C1右焦点的距离；

（2）求与双曲线C1有共同渐近线，且过点（-3，2）的双曲线C2的标准方程．

Answer 1

【答案】（1）4（2）x2-=1

【解析】

（1）由题得t2=12（-1）=15，再利用两点间的距离公式求得M点到双曲线C1右焦点的距离；（2）设双曲线C2的方程为-=m（m≠0，m≠1），代入点（-3，2），即得m的值和双曲线的标准方程.

解：（1）双曲线C1：-=1的右焦点为（4，0），

点M（3，t）在双曲线C1上，可得t2=12（-1）=15，

则M点到双曲线C1右焦点的距离为=4；

（2）与双曲线C1有共同渐近线，可设双曲线C2的方程为-=m（m≠0，m≠1），

代入点（-3，2），可得m=-=，

则双曲线C2的标准方程为x2-=1．