题目内容
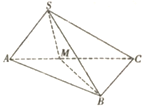
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a=2,c=3,又知bsinA=acos(B![]() ).
).
(Ⅰ)求角B的大小、b边的长:
(Ⅱ)求sin(2A﹣B)的值.
【答案】(Ⅰ)B![]() ,b
,b![]() ;(Ⅱ)
;(Ⅱ)![]()
【解析】
(1)将已知条件利用余弦的差角公式展开,再利用正弦定理将边化角,整理后得到角![]() ,再利用余弦定理,求得
,再利用余弦定理,求得![]() 边即可;
边即可;
(2)由(1)中所求,结合正弦定理,即可求得![]() ,再利用正弦的差角公式以及倍角公式展开代值计算即可.
,再利用正弦的差角公式以及倍角公式展开代值计算即可.
(Ⅰ)∵bsinA=acos(B![]() ).∴bsinA=a(
).∴bsinA=a(![]() cosB
cosB![]() sinB),
sinB),
∴由正弦定理可得sinBsinA=sinA(![]() cosB
cosB![]() sinB),∵sinA≠0,
sinB),∵sinA≠0,
∴sinBsinA=sinA(![]() cosB
cosB![]() sinB),可得sin(B
sinB),可得sin(B![]() )=0,
)=0,
∵B∈(0,π),B![]() ∈(
∈(![]() ,
,![]() ),
),
∴B![]() 0,可得B
0,可得B![]() .
.
∵a=2,c=3,
∴由余弦定理可得
b![]() .
.
(Ⅱ)∵B![]() ,a=2,b
,a=2,b![]() .∴由正弦定理
.∴由正弦定理![]() ,
,
可得sinA![]() ,cosA
,cosA![]() ,
,
sin2A=2sinAcosA![]() ,cos2A=2cos2A﹣1
,cos2A=2cos2A﹣1![]() ,
,
∴sin(2A﹣B)=sin2AcosB﹣cos2AsinB![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】给定整数![]() (
(![]() ),设集合
),设集合![]() ,记集合
,记集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() 构成以
构成以![]() 为首项,
为首项,![]() (
(![]() )为公差的等差数列,求证:集合
)为公差的等差数列,求证:集合![]() 中的元素个数为
中的元素个数为![]() ;
;
(3)若![]() 构成以
构成以![]() 为首项,
为首项,![]() 为公比的等比数列,求集合
为公比的等比数列,求集合![]() 中元素的个数及所有元素之和.
中元素的个数及所有元素之和.
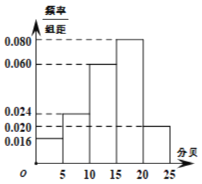
【题目】为了了解居民的家庭收入情况,某社区组织工作人员从该社区的居民中随机抽取了100户家庭进行问卷调查.经调查发现,这些家庭的月收入在3000元到10000元之间,根据统计数据作出如图所示的频率分布直方图:
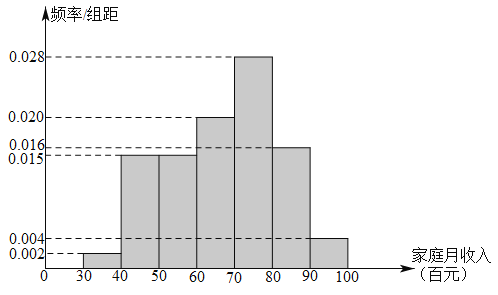
(1)经统计发现,该社区居民的家庭月收入![]() (单位:百元)近似地服从正态分布
(单位:百元)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.若
近似为样本平均数.若![]() 落在区间
落在区间![]() 的左侧,则可认为该家庭属“收入较低家庭”,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区
的左侧,则可认为该家庭属“收入较低家庭”,社区将联系该家庭,咨询收入过低的原因,并采取相应措施为该家庭提供创收途径.若该社区![]() 家庭月收入为4100元,试判断
家庭月收入为4100元,试判断![]() 家庭是否属于“收入较低家庭”,并说明原因;
家庭是否属于“收入较低家庭”,并说明原因;
(2)将样本的频率视为总体的概率.
①从该社区所有家庭中随机抽取![]() 户家庭,若这
户家庭,若这![]() 户家庭月收入均低于8000元的概率不小于50%,求
户家庭月收入均低于8000元的概率不小于50%,求![]() 的最大值;
的最大值;
②在①的条件下,某生活超市赞助了该社区的这次调查活动,并为这次参与调查的家庭制定了赠送购物卡的活动,赠送方式为:家庭月收入低于![]() 的获赠两次随机购物卡,家庭月收入不低于
的获赠两次随机购物卡,家庭月收入不低于![]() 的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
的获赠一次随机购物卡;每次赠送的购物卡金额及对应的概率分别为:
赠送购物卡金额(单位:元) | 100 | 200 | 300 |
概率 |
|
|
|
则![]() 家庭预期获得的购物卡金额为多少元?(结果保留整数)
家庭预期获得的购物卡金额为多少元?(结果保留整数)