��Ŀ����
����Ŀ��Ϊ���˽����ļ�ͥ���������ij������֯������Ա�Ӹ������ľ����������ȡ��100����ͥ�����ʾ�����.�����鷢�֣���Щ��ͥ����������3000Ԫ��10000Ԫ֮�䣬����ͳ������������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
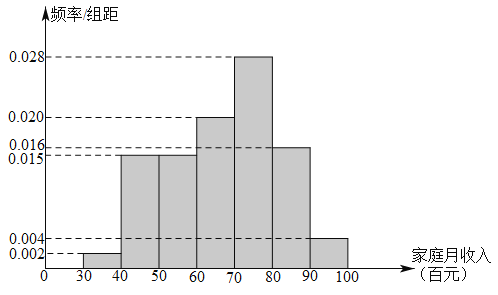
��1����ͳ�Ʒ��֣�����������ļ�ͥ������![]() ����λ����Ԫ�����Ƶط�����̬�ֲ�
����λ����Ԫ�����Ƶط�����̬�ֲ�![]() ������
������![]() ����Ϊ����ƽ����.��
����Ϊ����ƽ����.��![]() ��������
��������![]() ����࣬�����Ϊ�ü�ͥ��������ϵͼ�ͥ������������ϵ�ü�ͥ����ѯ������͵�ԭ����ȡ��Ӧ��ʩΪ�ü�ͥ�ṩ����;��.��������
����࣬�����Ϊ�ü�ͥ��������ϵͼ�ͥ������������ϵ�ü�ͥ����ѯ������͵�ԭ����ȡ��Ӧ��ʩΪ�ü�ͥ�ṩ����;��.��������![]() ��ͥ������Ϊ4100Ԫ�����ж�
��ͥ������Ϊ4100Ԫ�����ж�![]() ��ͥ�Ƿ�����������ϵͼ�ͥ������˵��ԭ��
��ͥ�Ƿ�����������ϵͼ�ͥ������˵��ԭ��
��2����������Ƶ����Ϊ����ĸ���.
�ٴӸ��������м�ͥ�������ȡ![]() ����ͥ������
����ͥ������![]() ����ͥ�����������8000Ԫ�ĸ��ʲ�С��50%����
����ͥ�����������8000Ԫ�ĸ��ʲ�С��50%����![]() �����ֵ��
�����ֵ��
���ڢٵ������£�ij����������˸���������ε�������Ϊ��β������ļ�ͥ�ƶ��������│�Ļ�����ͷ�ʽΪ����ͥ���������![]() �Ļ�������������│����ͥ�����벻����
�Ļ�������������│����ͥ�����벻����![]() �Ļ���һ��������│��ÿ�����͵Ĺ��│����Ӧ�ĸ��ʷֱ�Ϊ��
�Ļ���һ��������│��ÿ�����͵Ĺ��│����Ӧ�ĸ��ʷֱ�Ϊ��
�����│����λ��Ԫ�� | 100 | 200 | 300 |
���� |
|
|
|
��![]() ��ͥԤ�ڻ�õĹ��│���Ϊ����Ԫ�����������������
��ͥԤ�ڻ�õĹ��│���Ϊ����Ԫ�����������������
���𰸡���1��![]() ��ͥ������������ϵͼ�ͥ�������������2����
��ͥ������������ϵͼ�ͥ�������������2����![]() ��
��![]() Ԫ
Ԫ
��������
��1������Ƶ�ʷֲ�ֱ��ͼ���������������ļ�ͥ������ƽ��ֵ������![]() ���ȽϿɵã�
���ȽϿɵã�
��2������������Ƶ����Ϊ����ĸ��ʣ���������������8000Ԫ�ĸ��ʣ�����������¼��ĸ��ʹ�ʽ�õ�����ʽ����ü��ɣ����ɣ�1����֪�ü�ͥ�ɻ�������������│��������õĹ��│���Ϊ�������![]() ����
����![]() ��ȡֵ�ֱ�Ϊ200��300��400��500��600���ֱ��������ʣ�����������ɣ�
��ȡֵ�ֱ�Ϊ200��300��400��500��600���ֱ��������ʣ�����������ɣ�
�⣺��1������������ļ�ͥ������ƽ��ֵΪ��
![]() ����Ԫ��
����Ԫ��
����Ϊ����������ļ�ͥ������![]() ����λ����Ԫ�����Ƶط�����̬�ֲ�
����λ����Ԫ�����Ƶط�����̬�ֲ�![]()
����![]() ����
����![]()
������![]() ��ͥ������Ϊ4100Ԫ
��ͥ������Ϊ4100Ԫ![]() ��Ԫ
��Ԫ![]() ����
����![]() ��ͥ������������ϵͼ�ͥ��.
��ͥ������������ϵͼ�ͥ��.
��2���ٽ�������Ƶ����Ϊ����ĸ��ʣ���Ƶ�ʷֲ�ֱ��ͼ��֪����ȡһ����ͥ�����������8000Ԫ�ĸ���Ϊ![]()
�����ȡ![]() ����ͥ�����������8000Ԫ�ĸ���Ϊ
����ͥ�����������8000Ԫ�ĸ���Ϊ![]() ��������֪
��������֪![]() �����
�����![]()
���ɣ�1��֪![]() ��Ԫ
��Ԫ![]() Ԫ����
Ԫ����![]() ��ͥ���������
��ͥ���������![]() ���ɻ�������������│��������õĹ��│���Ϊ�������
���ɻ�������������│��������õĹ��│���Ϊ�������![]() ����
����![]() ��ȡֵ�ֱ�Ϊ200��300��400��500��600
��ȡֵ�ֱ�Ϊ200��300��400��500��600
![]() ��
��
![]() ��
��
��![]() ��ͥԤ�ڻ�õĹ��│���Ϊ
��ͥԤ�ڻ�õĹ��│���Ϊ![]() Ԫ.
Ԫ.

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�����Ŀ��ij�����ž��õķ�չ���������������������±��Ǹõ�һ����������������Ĵ��������������±�1��
���x | 2011 | 2012 | 2013 | 2014 | 2015 |
������y��ǧ��Ԫ�� | 5 | 6 | 7 | 8 | 10 |
Ϊ���о�����ķ��㣬������Ա���ϱ������ݽ����˴����� ![]() �õ��±�2��
�õ��±�2��
ʱ�����t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
������z����t�����Իع鷽�̣�
����ͨ���������еķ��̣����y����x�Ļع鷽�̣�
����������ع鷽��Ԥ�2020����ף��õش������ɴ���٣�
�������������Իع鷽��![]() ������
������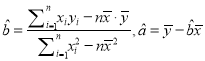 ��
��
����Ŀ��ijѧУΪ�˽��У�����꼶ѧ����ѧ��ѧϰ�������һģ������ѧ�ɼ����з��������г�ȡ��![]() ��ѧ���ijɼ���Ϊ��������ͳ�ƣ���Уȫ��ѧ���ijɼ�����
��ѧ���ijɼ���Ϊ��������ͳ�ƣ���Уȫ��ѧ���ijɼ�����![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ķ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��1����ʾ�������з�����
�ķ�������Ƶ�ʷֲ�ֱ��ͼ��ͼ��1����ʾ�������з�����![]() �ڵ��������ݵľ�Ҷͼ��ͼ��2����ʾ�������ϼ�ͳ�ƻ���Ԥ¼�����ߣ������з�������ܱ�¼ȡԺУ��ζ��ձ�Ϊ����3����
�ڵ��������ݵľ�Ҷͼ��ͼ��2����ʾ�������ϼ�ͳ�ƻ���Ԥ¼�����ߣ������з�������ܱ�¼ȡԺУ��ζ��ձ�Ϊ����3����
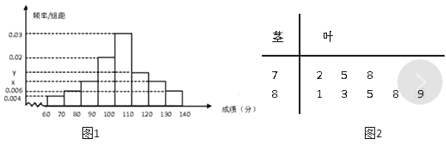
���� |
|
|
|
���ܱ�¼ȡԺУ��� | ר�� | ���� | �ر� |
ͼ��3��
��1����![]() ��Ƶ�ʷֲ�ֱ��ͼ�е�
��Ƶ�ʷֲ�ֱ��ͼ�е�![]() ��
��![]() ��ֵ��
��ֵ��
��2�������������������˼�룬���¼�������Ƶ����Ϊ���ʣ����ڸ�У�����꼶ѧ������ȡ3�ˣ���������һ���ǿ���¼ȡΪ�ر����ԺУ�ĸ��ʣ�
��3����ѡȡ�������У��ӿ���¼ȡΪ�ر���ר��������ε�ѧ���������ȡ3��ѧ�����е��У��ñ�ʾ����ȡ��3��ѧ����Ϊ�ر������������������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������