题目内容
【题目】已知平面内三个向量: ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1) (Ⅰ)若(
=(4,1) (Ⅰ)若( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),求实数k的值;
),求实数k的值;
(Ⅱ)设 ![]() =(x,y),且满足(
=(x,y),且满足( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),|
),| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求
,求 ![]() .
.
【答案】解:因为 ![]() =(3,2),
=(3,2), ![]() =(﹣1,2),
=(﹣1,2), ![]() =(4,1), 所以(Ⅰ)
=(4,1), 所以(Ⅰ) ![]() +k
+k ![]() =(3+4k,2+k),2
=(3+4k,2+k),2 ![]() ﹣
﹣ ![]() =(﹣5,2),又(
=(﹣5,2),又( ![]() +k
+k ![]() )∥(2
)∥(2 ![]() ﹣
﹣ ![]() ),
),
所以2(3+4k)+5(2+k)=0,解得k= ![]() ;
;
(Ⅱ) ![]() =(x,y),且满足(
=(x,y),且满足( ![]() +
+ ![]() )⊥(
)⊥( ![]() ﹣
﹣ ![]() ),|
),| ![]() ﹣
﹣ ![]() |=
|= ![]() ,又
,又 ![]() =(2,4),
=(2,4), ![]() =(x﹣4,y﹣1),
=(x﹣4,y﹣1),
所以 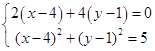 ,解得
,解得 ![]() 或
或 ![]()
所以 ![]() =(6,0)或者(2,2)
=(6,0)或者(2,2)
【解析】首先将它们中的相关向量坐标化,然后进行向量平行、垂直的坐标运算.
【考点精析】解答此题的关键在于理解平面向量的坐标运算的相关知识,掌握坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

