题目内容
7.求函数f(x)=$\frac{1}{2}$x2-(2+a)x+2alnx的单调区间.分析 先求出函数的导数,通过讨论a的范围,解关于导函数的不等式,从而求出函数的单调区间即可.
解答 解:∵f(x)=$\frac{1}{2}$x2-(2+a)x+2alnx,函数的定义域是(0,+∞),
∴f′(x)=x-(2+a)+$\frac{2a}{x}$=$\frac{(x-2)(x-a)}{x}$,
①a≤0时:令f′(x)>0,解得:x>2,令f′(x)<0,解得:0<x<2,
∴f(x)在(0,2)递减,在(2,+∞)递增;
②0<a<2时,令f′(x)>0,解得:x>2或x<a,令f′(x)<0,解得:a<x<2,
∴f(x)在(a,2)递减,在(0,a),(2,+∞)递增;
③a=2时:f′(x)≥0,f(x)在(0,+∞)递增;
④a>2时:令f′(x)>0,解得:x>a或x<2,令f′(x)<0,解得:2<x<a,
∴f(x)在(2,a)递减,在(0,2),(a,+∞)递增.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
15.某人射击一次,命中7-10环的概率如下表所示:
此人射击一次,命中不足8环的概率为0.42.
| 命中环数 | 10 | 9 | 8 | 7 |
| 概 率 | 0.12 | 0.18 | 0.28 | 0.32 |
12.已知函数ft(x)=-(x-t)2+t(t∈R),设a>b,f(x)=$\left\{\begin{array}{l}{{f}_{a}(x),{f}_{a}(x)≥{f}_{b}(x)}\\{{f}_{b}(x),{f}_{a}(x)<{f}_{b}(x)}\end{array}\right.$,若函数y=f(x)-x+a-b有四个零点,则b-a的取值范围是( )
| A. | (-∞,-2-$\sqrt{5}$) | B. | (-∞,2-$\sqrt{5}$) | C. | (-2-$\sqrt{5}$,0) | D. | (2-$\sqrt{5}$.0) |
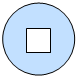 欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).
欧阳修《卖油翁》中写到:“(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔入,而钱不湿”.可见“行行出状元”,卖油翁的技艺让人叹为观止,如右图铜钱是直径为4cm的圆形,正中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油(油滴是直径为0.2cm的球),记“油滴不出边界”为事件A,“油滴整体正好落入孔中”为事件B.则P(B|A)=$\frac{64}{361π}$(不作近似值计算).