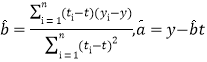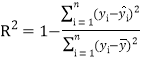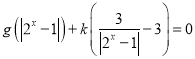题目内容
【题目】已知函数![]() 的定义域为
的定义域为![]() ,对任意实数
,对任意实数![]() ,都有
,都有![]() .
.
(1)若![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 为常数,函数
为常数,函数![]() 是奇函数,
是奇函数,
①验证函数![]() 满足题中的条件;
满足题中的条件;
②若函数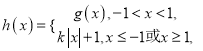 求函数
求函数![]() 的零点个数.
的零点个数.
【答案】(1) 解得![]() ,
, ![]() ;(2) ①见解析;② 当
;(2) ①见解析;② 当![]() 时,函数
时,函数![]() 只有1零点;
只有1零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有3零点;当
有3零点;当![]() 是,函数
是,函数![]() 有5零点.
有5零点.
【解析】试题分析:(1)由题意,取![]() ,得
,得![]() ,再取
,再取![]() ,得
,得![]() ,
,
即函数![]() 在
在![]() 内为奇函数,代入化简即可求解
内为奇函数,代入化简即可求解![]() 的值.
的值.
(2)由函数![]() 是奇函数,得
是奇函数,得![]() ,得出
,得出![]() 的解析式,进而求解
的解析式,进而求解![]() .
.
再由![]() ,得
,得![]() ,令
,令![]() ,则
,则![]() ,作出图象,进而分类讨论,求得函数零点的个数.
,作出图象,进而分类讨论,求得函数零点的个数.
试题解析:
(1)对题中条件取![]() ,得
,得![]() .
.
再取![]() ,得
,得![]() ,则
,则![]() ,
,
即函数![]() 在
在![]() 内为奇函数.
内为奇函数.
所以![]() ,
,
又![]() .
.
解得![]() ,
, ![]() .
.
(2)由函数![]() 是奇函数,得
是奇函数,得![]() ,则
,则![]() .
.
此时![]() ,满足函数
,满足函数![]() 是奇函数,且
是奇函数,且![]() 有意义.
有意义.
①由![]() ,得
,得![]() ,则对任意实数
,则对任意实数![]() ,
,
有![]()
![]() ,
,

![]() ,
,
所以![]() .
.
②由![]() ,得
,得![]() ,令
,令![]() ,则
,则![]() .
.
作出图象
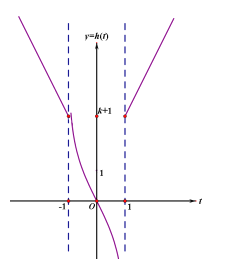
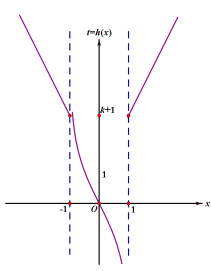
由图可知,当![]() 时,只有一个
时,只有一个![]() ,对应有3个零点;
,对应有3个零点;
当![]() 时,只有一个
时,只有一个![]() ,对应只有一个零点;
,对应只有一个零点;
当![]() 时,
时, ![]() ,此时
,此时![]() ,
, ![]() ,
, ![]() .
.
由![]()
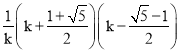
得在![]() 时,
时, ![]() ,三个
,三个![]() 分别对应一个零点,共3个.
分别对应一个零点,共3个.
在![]() 时,
时, ![]() ,三个
,三个![]() 分别对应1个,1个,3个零点,共5个.
分别对应1个,1个,3个零点,共5个.
综上所述,当![]() 时,函数
时,函数![]() 只有1零点;
只有1零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有3零点;
有3零点;
当![]() 是,函数
是,函数![]() 有5零点.
有5零点.

练习册系列答案
相关题目