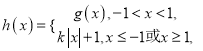题目内容
【题目】已知函数![]() ,在
,在![]() 处有最小值为0.
处有最小值为0.
(1)求![]() 的值;
的值;
(2)设![]() ,
,
①求![]() 的最值及取得最值时
的最值及取得最值时![]() 的取值;
的取值;
②是否存在实数![]() ,使关于
,使关于![]() 的方程
的方程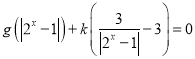 在
在![]() 上恰有一个实数解?若存在,求出实数
上恰有一个实数解?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由二次函数的性质,得到顶点式![]() ,求出
,求出![]() 的值;(2)令
的值;(2)令![]() ,利用复合函数的性质得到
,利用复合函数的性质得到![]() 的最值及对应的
的最值及对应的![]() 的取值;
的取值; ![]() ,整理得
,整理得![]() ,利用二次函数的根的分布,因为恰有一个实数解,根据
,利用二次函数的根的分布,因为恰有一个实数解,根据![]() 的性质,则有两个相等的大于1的根或有两个不相等的根
的性质,则有两个相等的大于1的根或有两个不相等的根![]() ,
, ![]() ,结合二次函数图象写出约束条件,解出答案。
,结合二次函数图象写出约束条件,解出答案。
试题解析:
(1)![]() ,所以
,所以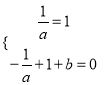 ,得
,得![]() .
.
(2)![]() ,①令
,①令![]() ,则
,则![]() ,
, ![]() 在
在![]() 递减,
递减, ![]() 递增,所以
递增,所以![]() ,此时
,此时![]() ,
, ![]() ,此时
,此时![]() .
.
②令![]() ,则
,则![]() ,即
,即![]()
![]()
,
方程![]() 有两个相等的大于1的根,则
有两个相等的大于1的根,则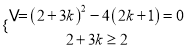 ,得
,得![]() ;
;
方程![]() 有两个根
有两个根![]() ,
, ![]() ,则
,则![]() ,得无解,
,得无解,
综上所述,存在这样的![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目