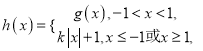题目内容
【题目】已知函数 ,函数
,函数![]()
![]() (a>0),
(a>0),
若存在![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】∵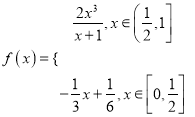 ,
,
①当x∈[0, ![]() ]时,f(x)=
]时,f(x)= ![]() 在R上是单调递减函数,
在R上是单调递减函数,
∴f(![]() )f(x)f(0),即0f(x)
)f(x)f(0),即0f(x) ![]() ,
,
∴f(x)的值域为[0, ![]() ];
];
②当x∈(![]() ,1]时,f(x)=
,1]时,f(x)= ![]() ,
,
∴f′(x)= ![]() =
=![]() ,
,
∴当x>![]() 时,f′(x)>0,即f(x)在(
时,f′(x)>0,即f(x)在(![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴f(x)在(![]() ,1]上单调递增,
,1]上单调递增,
∴f(![]() )<f(x)f(1),即
)<f(x)f(1),即![]() <f(x)1,
<f(x)1,
∴f(x)的值域为[![]() ,1].
,1].
综合①②,f(x)的值域为[0,1].
∵g(x)=asin(![]() )2a+2,(a>0),且x∈[0,1],
)2a+2,(a>0),且x∈[0,1],
∴0![]() x
x![]() ,则0sin(
,则0sin(![]() x)
x) ![]() ,
,
∵a>0,则0asin(![]() x)
x) ![]() a,
a,
∴22ag(x)2![]() a,
a,
∴g(x)的值域为[22a,2![]() a],
a],
∵存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,
∴[0,1]∩[22a,2![]() a]≠,
a]≠,
若[0,1]∩[22a,2![]() a]=,则2
a]=,则2![]() a<0或22a>1,
a<0或22a>1,
∴a<![]() 或a>
或a>![]() ,
,
∴当[0,1]∩[22a,2![]() a]≠时,a的取值范围为[12,
a]≠时,a的取值范围为[12, ![]() ],
],
∴实数a的取值范围是[![]() ,
,![]() ].
].
故答案为:D.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
【题目】某地区2008年至2014年中,每年的居民人均纯收入y(单位:千元)的数据如下表:
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验,得知t与y之间具有线性相关关系.
(1)求y关于t的线性回归方程;
(2)预测该地区2017年的居民人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
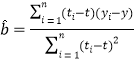 ,
,![]()