题目内容
【题目】有一块扇形铁皮OAB,∠AOB=60°,OA=72cm,要剪下来一个扇环形ABCD,作圆台容器的侧面,并且在余下的扇形OCD内能剪下一块与其相切的圆形使它恰好作圆台容器的下底面(大底面).试求:
(1)AD应取多长?
(2)容器的容积为多大?
【答案】（1）36；（2）
【解析】试题分析：（1）设圆台上、下底面半径分别为
，则
，由题意得
，由此能求出
长．
（2）圆台所在圆锥的高
，圆台的高
，由此能求出容器的容积．
试题解析;(1)如图,设圆台上、下底面半径分别为r,R,AD=xcm,则OD=(72-x)cm.
由题意得
所以R=12,r=6,x=36,所以AD=36cm.
(2)圆台所在圆锥的高H=
=12
,圆台的高h=
=6
,小圆锥的高h'=6
,
所以V容=V大锥-V小锥=
πR2H-
πr2h'=504
π.
练习册系列答案
53随堂测系列答案
相关题目
【题目】某地区2008年至2014年中，每年的居民人均纯收入y（单位：千元）的数据如下表：
年 份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.7 | 3.6 | 3.3 | 4.6 | 5.4 | 5.7 | 6.2 |
对变量t与y进行相关性检验，得知t与y之间具有线性相关关系．
（1）求y关于t的线性回归方程；
（2）预测该地区2017年的居民人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
，
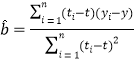