题目内容
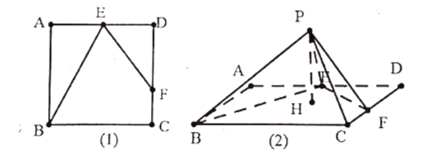
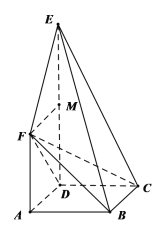
【题目】如图,在多面体![]() 中,正方形
中,正方形![]() 与梯形
与梯形![]() 所在平面互相垂直,已知
所在平面互相垂直,已知![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由正方形的性质及平面![]()
![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,即
,即![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证得
,可证得![]() ,即可求证;
,即可求证;
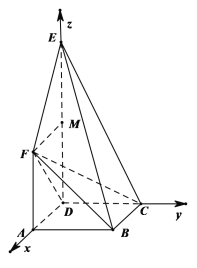
(2)以![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,由(1)可得
,由(1)可得![]() 为平面
为平面![]() 的一个法向量,再求得平面
的一个法向量,再求得平面![]() 的一个法向量
的一个法向量![]() ,进而利用余弦定理求解即可.
,进而利用余弦定理求解即可.
(1)证明:![]() 正方形
正方形![]() ,
,![]() ,
,
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,易得四边形
,易得四边形![]() 为正方形,
为正方形,![]() ,
,
则![]() ,即
,即![]() ,
,
又![]() ,则
,则![]() 平面
平面![]() .
.
(2)![]() 且
且![]() ,
,![]() ,
,
又![]() 平面
平面![]() ,易知
,易知![]() 两两垂直,
两两垂直,
以![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图所示,
,如图所示,
易得![]() ,则
,则![]() ,
,![]() ,
,
由(1)得![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
令![]()
![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则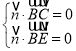 ,得
,得![]() ,
,
不妨令![]() ,则
,则![]() ,故
,故![]()
![]() ,
,
令所求二面角为![]() ,则
,则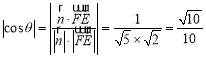 ,
,
则![]()

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中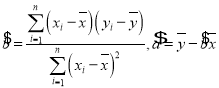 )
)