Question

【题目】在直角坐标系中，曲线的参数方程为（为参数），将曲线上各点纵坐标伸长到原来的倍（横坐标不变），得到曲线.以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

（1）写出曲线的极坐标方程与直线的直角坐标方程；

（2）曲线上是否存在不同的两点，（以上两点坐标均为极坐标，，，，），使点、到的距离都为？若存在，求出的值；若不存在，请说明理由.

Answer 1

【答案】（1），；（2）存在，

【解析】

（1）首先根据题意求出曲线的参数方程为（为参数），从而得到直角坐标方程，再转化为极坐标方程即可.根据，，将直线的极坐标方程转化为直角坐标方程即可.

（2）首先计算曲线的圆心到直线的距离，结合图象得到存在这样的点，再利用极坐标计算的值即可.

（1）由曲线的参数方程为（为参数），

将曲线上各点纵坐标伸长到原来的倍（横坐标不变），

得到曲线的参数方程为（为参数），

得到曲线的直角坐标方程为，其极坐标方程为，

又直线的极坐标方程为，

故其直角坐标方程为.

（2）曲线是以为圆心，为半径的圆，

圆心到直线的距离，

所以存在这样的点，，且点到直线的距离为，

如图所示：

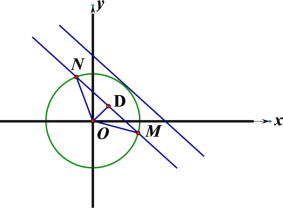
因为，所以，

即：.

又因为，，，

所以.